Torsional Rigidity: Classical and new results
Torsional rigidity is a key quantity to characterize how a beam responds to applied forces. The higher the torsional rigidity, the harder it is to deform the beam. A natural question arises: which shape for the beam’s cross section yields the highest torsional rigidity? The answer was conjectured to be a circle by Saint-Venant back in 1856, but the question remains the source of interesting mathematics. Here, we report some of the latest perspectives.
Torsional rigidity and the Saint Venant inequality
Let \Omega \subset \mathbb{R}^2 be an open and bounded set that represents the beam’s cross section, as sketched in Figure 1. The torsional rigidity of \Omega (that is, of the beam) can be calculated as
T(\Omega):=\int_\Omega u(x)\, dx, \qquad (1)
where the function u(x) is the unique solution of the problem
\begin{cases} -\Delta u=1 \, &\text{in } \Omega, \\ u=0 & \text{on } \partial\Omega. \qquad (2) \end{cases}

Figure 1. Sketch of a beam with cross section \Omega.
Write |\Omega| for the area of \Omega. The following theorem, proved in [7], states mathematically that the highest torsional rigidity is obtained when \Omega is a circle.
Theorem 1.1
Let B\subset \mathbb{R}^2 be a disk and let \Omega\subset\mathbb{R}^2 be an open, bounded set with |\Omega|=|B|. Then,
T(\Omega)\leq T(B) \qquad (3)
and the equality is attained if and only if \Omega=B.
Inequality (3), known as the Saint Venant inequality, tells us that every choice of \Omega that is not a disk leads to a loss of torsional rigidity. How large can this loss be? In other words, can we estimate how large the difference T(B)-T(\Omega) is given some measure of how far \Omega is from being a disk?
One way to answer this question is to introduce the so-called Fraenkel asymmetry,
\mathcal{A}(\Omega):=\min_{x \in \R^{2}}\bigg \{ \dfrac{|\Omega\triangle B(x)|}{|B(x)|)} \;,\; |B(x)|=|\Omega|\bigg \},
where B(x) is the disk centred at x with the same area as \Omega and \triangle denotes the symmetric difference between sets.
The following sharp quantitative version of Saint Venant’s inequality (3) was proved recently in [2].
Theorem 1.2
Let \Omega\subset\mathbb{R}^2 be an open, bounded set. Then, there exists C>0 such that
T(B)-T(\Omega)\geq C \mathcal{A}^2(\Omega). \qquad (4)
Estimates on the torsional rigidity
We turn turn to estimating the actual value of T(\Omega), rather than its difference from the optimal value T(B). We will consider sets \Omega\subset\mathbb{R}^2 that are open, bounded and convex, and we write |\Omega| and P(\Omega) for their area and perimeter, respectively.
Rather than measure T(\Omega) directly, which depends on how the precise size of \Omega (thick bars are clearly more rigid than thin ones!), it is desirable to consider a scale invariant measure of torsional rigidity. A suitable choice is the quantity
\frac{T(\Omega)P^2(\Omega)}{ |\Omega|^3}.
Note that it is scaling invariant because, for every t>0, we have
P(t\Omega)= tP(\Omega), |t\Omega|= t^2 |\Omega| and T(t\Omega)=
t^3 T(\Omega). The following lower and upper bounds were proved, respectively, by P\’olya in [8] and by Makai in [6].
Theorem 2.1
Let \Omega\subset\mathbb{R}^2 an open, bounded and convex set. Then,
\frac{1}{3} \leq\frac{T(\Omega)P^2(\Omega)}{|\Omega|^3} \leq \frac{2}{3}. \qquad (5)
Moreover, the lower bound is asymptotically achieved by a sequence of thinning rectangles and the upper bound is asymptotically achieved by a sequence of thinning triangles.
Quantitative estimates for beams with convex cross-section
As for Saint Venant’s inequality, it makes sense to ask how far a certain cross-sectional shape \Omega is from saturating the bounds in (5). One challenge is that the upper and lower bounds are never achieved by any shape, but are only approached asymptotically by so-called thinning domains. The definition of thinning domains relies on two key geometric quantities:
• The diameter of \Omega, denoted by {\rm diam}(\Omega). This is the maximal distance between two points in \partial\Omega.
• The minimal width of \Omega, denoted by w(\Omega). This is the minimal distance between two parallel supporting hyperplanes (see Figure 2).
Definition 3.1
Let \Omega_k be a sequence of open, bounded and convex sets of \mathbb{R}^2 with constant area |\Omega_k|. We say that \Omega_k is a sequence of thinning domains if
\dfrac{w(\Omega_k)}{ diam(\Omega_k) }\xrightarrow{k \to 0}0.
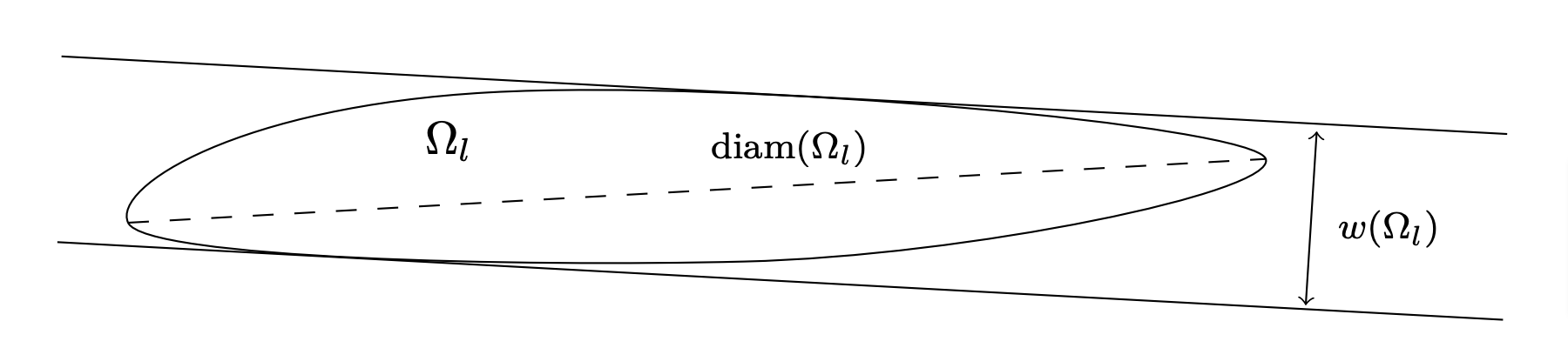
Figure 2. Minimal width and diameter of a convex set.
In our work [1], we obtain the following quantitative versions of the inequalities in (5).
Theorem 3.1
Let \Omega\subset\mathbb{R}^2 be an open, bounded and convex set. There exists a constant C>0 such that
\dfrac{T(\Omega)P(\Omega)^2}{|\Omega|^3}-\frac{1}{3}\ge C \frac{w(\Omega)}{{\rm diam}(\Omega)}. \qquad (6)
Theorem 3.2
Let \Omega be an open bounded and convex set, then there exists a constant K>0 such that
\dfrac{T(\Omega)P(\Omega)^2}{|\Omega|^3}-\frac{1}{3}\ge K \left(\frac{|Q \setminus \Omega|}{|\Omega|}\right)^3, \qquad (7)
where Q is a rectangle of sides P(\Omega)/ 2 and w(\Omega), containing \Omega (see Figure 3).

Figure 2. Rectangle with sides P(\Omega)/2 and w_{\Omega} containing \Omega.
Theorem 3.1 tells us that if the sequence of convex planar domains (\Omega_k)_{\{k>0\}} is such that
\dfrac{T(\Omega_k)P(\Omega_k)^2}{|\Omega_k|^3}-\frac{1}{3}\to 0,
then (\Omega_k)_{\{k>0\}} must be a sequence of thinning domains
Theorem 3.2, instead, is more precise: it says that if
\dfrac{T(\Omega_k)P(\Omega_k)^2}{|\Omega_k|^3}-\frac{1}{3}\to 0,
then (\Omega_k)_{\{k>0\}} is a sequence of thinning domains “near” to a sequence of thinning rectangles. Precisely, there exists a sequence of thinning rectangles (Q_k)_{\{k>0\}}, defined as in the statement of Theorem 3.2, such that \Omega_k \subseteq Q_k and
\dfrac{|Q_k\setminus \Omega_k|}{|\Omega_k|} \to 0. \qquad (8)
The quantity on the left-hand-side of (8) can be considered a measure of asymmetry with respect to the thinning rectangular shapes.
Further results and open problems
The definition of Torsional Rigidity (1) can be given in dimension n>2 and the Saint-Venant inequality (3) and the relative quantitative results still hold. As far as the bounds on T(\Omega) in terms of perimeter and volume are concerned, it was recently proven in [3] that P\’olya inequality still holds in \mathbb{R}^n and it is asymptotically achieved for thinning cylinders (the natural generalisation in dim n>2 of the thinning rectangles). The generalisation to higher dimension of Makai’s results is still an open problem (see [3] for the relative conjecture, where the authors solve the problem only in the class of convex, thinning domains).
One can also define a notion of torsional rigidity when the Laplacian operator in (2) is replaced with the p-Laplacian
-\Delta_p u:=-{\rm div}\left(|\nabla u|^{p-2}\nabla u\right)\qquad p\in(1,+\infty).
In this case one can generalize the Saint-Venant inequality, its quantitative version, the P\’olya inequality in dimension n\geq 2 (see [5] for the planar case and [4] for the general one) and Makay’s results in the planar case (see [5]).
Finally, Theorem 3.1 can be generalized to dimension greater than 2 and for the p-Laplacian. We are currently working on a similar generalisation of Theorem 3.2.
References
[1] V. Amato, A. L. Masiello, G. Paoli, and R. Sannipoli. Sharp and quantitative estimates for the p-Torsion of convex sets. NoDEA Nonlinear Differential Equations Appl., 30(1):Paper No. 12, 22, 2023.
[2] Lorenzo Brasco, Guido De Philippis, and Bozhidar Velichkov. Faber-Krahn inequalities in sharp quantitative form. Duke Math. J., 164(9):1777–1831, 2015.
[3] Luca Briani, Giuseppe Buttazzo, and Francesca Prinari. Some inequalities involving perimeter and torsional rigidity. Applied Mathematics & Optimization, pages 1–15, 2020.
[4] Francesco Della Pietra and Nunzia Gavitone. Sharp bounds for the first eigenvalue and the torsional rigidity related to some anisotropic operators. Math. Nachr., 287(2-3):194–209, 2014.
[5] Ilaria Fragalà, Filippo Gazzola, and Jimmy Lamboley. Sharp bounds for the p-torsion of convex planar domains. In Geometric properties for parabolic and elliptic PDE’s, volume 2 of Springer INdAM Ser., pages 97–115. Springer, Milan, 2013.
[6] Endre Makai. On the principal frequency of a membrane and the torsional rigidity of a beam. In Studies in mathematical analysis and related topics, pages 227–231. Stanford Univ. Press, Stanford, Calif., 1962.
[7] G. Pólya and G. Szegö. Isoperimetric Inequalities in Mathematical Physics. Annals of Mathematics Studies, no. 27. Princeton University Press, Princeton, N. J., 1951.
[8] George Pólya. Two more inequalities between physical and geometrical quantities. J. Indian Math. Soc. (N.S.), 24:413–419 (1961), 1960.
|| Go to the Math & Research main page