[Past member] Research Group Leader | Senior Scientist (2021 – 2024)
yue.wang@fau.de
Room 03.319 | Friedrich-Alexander-Universität Erlangen-Nürnberg. FAU DCN-AvH Chair for Dynamics, Control, Machine Learning and Numerics – Alexander von Humboldt Professorship.
+49 9131 85-67131
Hi, I am Yue from China. I got my Bachelor degree (2015) and Doctor degree (2019) in Mathematics and Applied Mathematics from Fudan University, Shanghai. My field of expertise is in the area of Control Theory for PDEs in Applications, especially for Hyperbolic Systems and related topics in Modeling, Analysis and Control Design, Sychronization. In 2019, I arrived in Germany for DFG L595/31-1 project at FAU.
From Sep. 2021, I am at the Chair for Dynamics, Controls, Machine Learning and Numerics. My interest is Controls on Networks: Modeling, Learning and Applications.
I am always loving Mathematics – it opens a window onto the order of nature hidden – brings me a story of life to understand the world I am in – and involves me in it emotionally and intellectually.
Hope to meet you in future.
PhD Thesis: Exact boundary Controllability for Wave Equations with Dynamical Boundary Conditions and of Partial Nodal Profile for Wave Equation (June 6, 2019)
Events
• October 7-10, 2024. CIN-PDE 2024. Lecture: “Exact Boundary Controllability of a Timoshenko Beam” (G. Leugering, Y. Wang). Conference on Control, Inversion and Numerics for PDEs (Fudan University, Shanghai)
• June 10-14, 2024. Trends in Mathematical Sciences. #TrendsInMaths conference (Erlangen)
• September 27, 2023. Random Batch Methods for Optimal Control of 1D Hyperbolic Systems. EUCCO 2023, Heidelberg
• August 1-4, 2023. CIN-PDE 2023 • Erlangen-Shanghai: Workshop on Control, Inversion and Numerics for PDEs
Projects
- DFG WA5144/1-1: Analysis and Control of Nonlinear Hyperbolic Systems with Degeneration on Networks (2022-2024)
- ETI; Approximating Steady-State Maxwell’s Equations via Physics-Informed Neural Networks (2022-2024)
My posts on Math & Research

Nonlinear hyperbolic systems: Modeling, controllability and applications
My posters

Boundary Controllability of Nodal Profile for Hyperbolic Systems
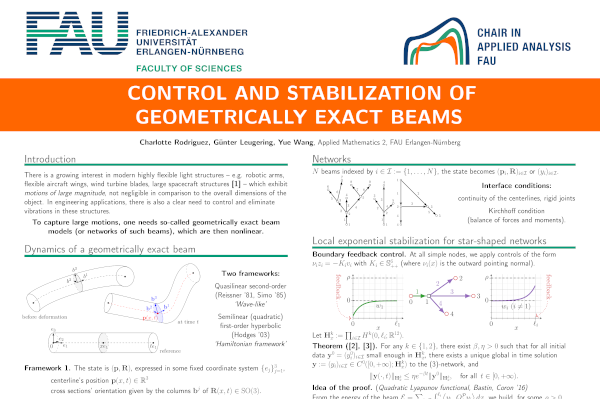
Control and Stabilization of Geometrically Exact Beams C
Publications
2022
- , , , :
Controllability properties of a hyperbolic system with dynamic boundary conditions
In: Journal of Evolution Equations 22 (2022)
ISSN: 1424-3199
DOI: 10.1007/s00028-022-00823-5
BibTeX: Download
2021
- , , :
Nodal profile control for networks of geometrically exact beams
In: Journal De Mathematiques Pures Et Appliquees (2021)
ISSN: 0021-7824
DOI: 10.1016/j.matpur.2021.07.007
BibTeX: Download - , , :
Boundary controllability of a system modelling a partially immersed obstacle
In: Esaim-Control Optimisation and Calculus of Variations 27 (2021)
ISSN: 1292-8119
DOI: 10.1051/cocv/2021076
BibTeX: Download - , :
Exact boundary controllability of partial nodal profile for network of strings
In: Nonlinear Analysis-Real World Applications 62 (2021), Article No.: 103383
ISSN: 1468-1218
DOI: 10.1016/j.nonrwa.2021.103383
BibTeX: Download
2020
- , , :
Exact Boundary Controllability for the Spatial Vibration of String with Dynamical Boundary Conditions
In: Chinese Annals of Mathematics Series B 41 (2020), p. 325-334
ISSN: 0252-9599
DOI: 10.1007/s11401-020-0201-1
URL: https://link.springer.com/article/10.1007/s11401-020-0201-1
BibTeX: Download
2019
- , , , :
A NOTE on WEIGHTED SOBOLEV SPACES RELATED to WEAKLY and STRONGLY DEGENERATE DIFFERENTIAL OPERATORS
In: Journal of Optimization, Differential Equations and Their Applications 27 (2019), p. 1-22
ISSN: 2312-4547
DOI: 10.15421/141905
BibTeX: Download - , , :
1-d Wave Equations Coupled via Viscoelastic Springs and Masses: Boundary Controllability of a Quasilinear and Exponential Stabilizability of a Linear Model
In: Springer INdAM Series, Springer International Publishing, 2019, p. 139-156 (Springer INdAM Series, Vol.32)
DOI: 10.1007/978-3-030-17949-6_8
BibTeX: Download - , , :
Exact boundary controllability and its applications for a coupled system of quasilinear wave equations with dynamical boundary conditions
In: Nonlinear Analysis-Real World Applications 49 (2019), p. 71-89
ISSN: 1468-1218
DOI: 10.1016/j.nonrwa.2019.02.006
BibTeX: Download
2016
- , , :
Exact boundary controllability for 1-D quasilinear wave equations with dynamical boundary conditions
In: Mathematical Methods in the Applied Sciences 40 (2016), p. 3808-3820
ISSN: 0170-4214
DOI: 10.1002/mma.4265
URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/mma.4265
BibTeX: Download






