A relaxed splitting method for solving variational inclusion and fixed point problems
1 Introduction
Variational inclusion and fixed point problems are fundamental in many areas of applied mathematics, including optimization, inverse problems, equilibrium theory, image processing, and machine learning. These problems can be formulated as finding a common solution u^* in a real Hilbert space H such that
\text{Find} \, u^{*} \in H, \quad \text{such that} \, 0 \in \left( A_1 + A_2 \right)(u^{*}), \quad \text{and} \quad u^*=G(u^*),
where A_1 : H \rightarrow H is a single-valued monotone operator, A_2 : H \rightarrow 2^H is a multi-valued maximal monotone operator, and G : H \rightarrow H is a pseudo-contractive mapping. These problems naturally arise in modeling various real-world applications, such as signal recovery, deblurring of images, and the design of equilibrium systems in networks.
Classical algorithms, such as the forward-backward splitting method and the forward-reflected-backward splitting method, have been widely applied to solve these problems. However, these methods rely on strong assumptions like cocoercivity or the availability of Lipschitz constants for the operators, which may not hold in many practical scenarios. For example, in large-scale image reconstruction tasks, the Lipschitz constants are often unknown or too costly to compute.
To overcome these limitations, it is essential to design iterative methods that are more flexible and can still guarantee convergence under milder conditions. Motivated by this need, we propose a relaxed splitting algorithm that incorporates inertial steps and adaptive step sizes. This approach not only weakens the restrictive assumptions of earlier methods but also improves computational efficiency and practical performance in solving complex variational inclusion and fixed point problems.
2 Background
Classical splitting methods are commonly used to solve problems of the form
\text{Find } u^* \in H \text{ such that } 0 \in (A_1 + A_2)(u^*), (1)
where A_1 : H \to H is a single-valued monotone operator and A_2 : H \to 2^H is a maximal monotone operator.
One of the basic methods is the forward-backward splitting algorithm, which generates a sequence (u_n) as follows:
u_{n+1} = J_{\eta A_2}(u_n - \eta A_1u_n), (2)
where J_{\eta A_2} = (I + \eta A_2)^{-1} is the resolvent of A_2 and \eta > 0 is a fixed parameter. This method requires A_1 to be cocoercive, which is a strong assumption.
To overcome this limitation, Tseng proposed the forward-backward-forward (FBF) method, defined by
\bar{u}_n = J_{\eta A_2}(u_n - \eta A_1u_n), (3)
u_{n+1} = \bar{u}_n - \eta(A_1\bar{u}_n - A_1u_n). (4)
This method relaxes the cocoercivity condition but requires an additional evaluation of A_1 in each iteration, which can be computationally expensive.
Later, Malitsky [2] introduced the forward-reflected-backward (FRB) method:
u_{n+1} = J_{\eta A_2}\big(u_n - \eta(A_1u_n + A_1(u_n - u_{n-1}))\big). (5)
This method removes the cocoercivity assumption and reduces the number of operator evaluations.
In this work, we are interested in finding a common solution of the variational inclusion problem and the fixed point problem:
u^* \in C \text{ such that } u^* = G(u^*), (6)
where G : H \to H is a pseudo-contractive mapping.
3 Main Results
A Self-adaptive Inertial Algorithm for Solving Variational Inclusion and Fixed Point Problems for Pseudocontractive Mapping
We propose an accelerated self adaptive iteration for pseudocontractive mapping by incorporating the inertial extrapolation step with algorithm of Yao et al. [1]. The purpose of this modification is to obtain a self adaptive scheme with strong convergence properties, maximally monotone and monotone as the underlying operator.
Assumption 1
(A1) The solution set \Omega of the common solution of variational inclusion and fixed point problem is nonempty.
(A2) Let the operator A_{1} : H \longrightarrow H be L_2-Lipschitz continuous and monotone and A_{2} : H \longrightarrow 2^{H} be a maximal monotone operator with dom(g) \subset H.
(A3) Let G: H \longrightarrow H be an L_1-Lipchitz and pseudo-contractive operator with L_1 > 1.
We now present the proposed self-adaptive algorithm involving a maximally monotone and a monotone operator and a fixed point of a pseudocontractive mapping.
Algorithm 1
A Relaxed Inertial Algorithm for Inclusion and Fixed point Problems
Initialization: Let x,u_0 \in H , \mu \in (0,1) ,\eta_{0} > 0,\kappa , \rho ,\hat{\theta} > 0 and \left\{\theta_n\right\} \subset [0,1), \left\{\xi_n \right\} \subset (0,1) such that 0 \lt \kappa \leq \rho \lt (1/\sqrt{1+L^2}+1), 0 \leq \theta_n \leq \hat{\theta} \lt 1. Set n = 0.
Iterative Steps 1: For given u_{n}, compute w_{n} by
w_{n} = u_{n}+\theta _{n}(u_{n}-u_{n-1}). (7)
Step 2: For given w_{n}, compute v_{n} by
v_{n} = (1- \kappa )w_{n}+\kappa G[((1-\varrho )w_{n}+\varrho Gw_{n})]. (8)
Step 3:
For given v_{n}, compute z_{n} by
z_{n}= J_{\eta _{n}}^{A_{2}}(I-{\eta_{n}}A_{1})v_n. (9)
Step 4:
Compute u_{n+1} by
u_{n+1} = x\xi_n +(1-\xi _{n})[z_n -\eta_{n}(A_{1}z_{n}-A_{1}v_{n})] . (10)
Step 5:
Set n: = n+1 and return to Step 1.
The step-size is chosen by
\eta_{n+1}=\begin{cases} \min \left \{\frac{\mu\left\| z_n - v_n\right\|}{\left\|Az_n - Av_n \right\|} ,\eta_n \right \}, & \text{if} Az_n - Av_n \neq 0;\\ \eta_n, & \text{otherwise} \end{cases} (11)
Assume that the setting (A1-A3) are satisfied and let the sequence \left\{\xi_n\right\} \subset (0,1) such that \lim _{n \rightarrow \infty} \xi_n=0 and \sum_{n=1}^{\infty} \xi_n=\infty and let \kappa , \rho > 0 such that 0 \lt \kappa \leq \rho \lt (1/\sqrt{1+L^2}+1). Then, the sequence \left\{u_n\right\} generated by Algorithm 1 converges strongly to P_{\Omega}(x).
4 Numerical Experiments
We investigate the results of Algorithm 1 and compare it with algorithms proposed by Raweerote Suparatulatorn and Anchalee Khemphet [3] (Algorithm 2), and Aviv Gibali and Duong Viet Thong [1] (Algorithm
3).
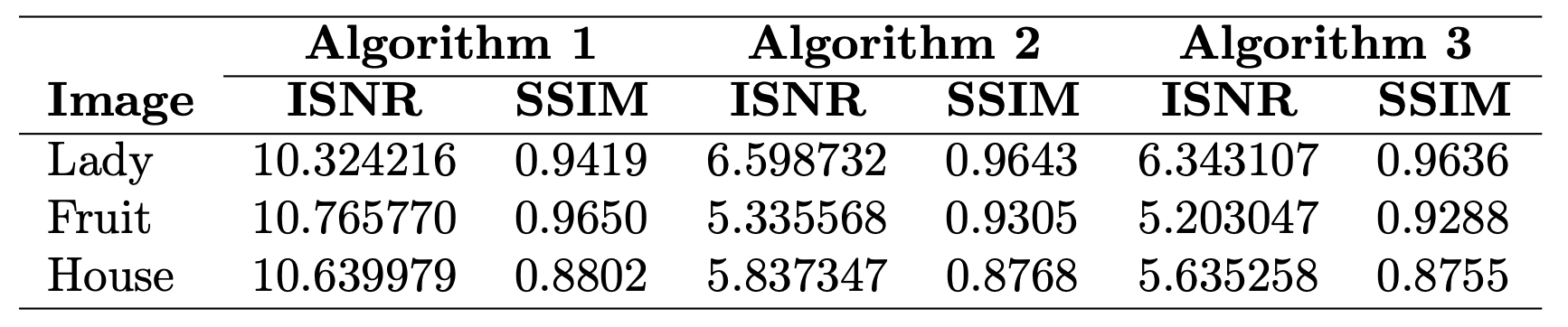
Table 1. The ISNR and SSIM values of the compared algorithms.
We apply the method to image recovery tasks and compare the results against existing algorithms. The numerical results show that our algorithm outperforms the competitors in terms of ISNR and SSIM, demonstrating its practical effectiveness in real-world applications.
4.1 An example in L_2 ([0,1])
Example 1. In L_2 ([0,1]), we set
A_1 x (t) := x(t), \quad A_2 x (t) := 2x(t), \quad Gx(t) := gx(t).
It can be observed that A_1 is monotone, A_2 is maximal monotone and G is nonexpansive. Consequently, the solution set is \Omega = F(G) \cap (A_1 + A_2)^{-1} (0) = \left\{0 \right\}. In Algorithm 1, the parameters are set as \kappa = 0.6, \varrho = 0.7, \xi_n = \frac{1}{(100k+1)} , for all k \in N. For comparison, in the algorithms 2 and 3 , let \lambda = 0.5 ,\alpha_k = \frac{1}{(k+1)} , \beta_k = \frac{k}{(2k+1)}, for all k \in N .
In all cases, the control parameter \mu= 0.85 . The maximum number of iterations is n=5, with a tolerance of 10^{-5}. See Table 2 for the results of the simulations.
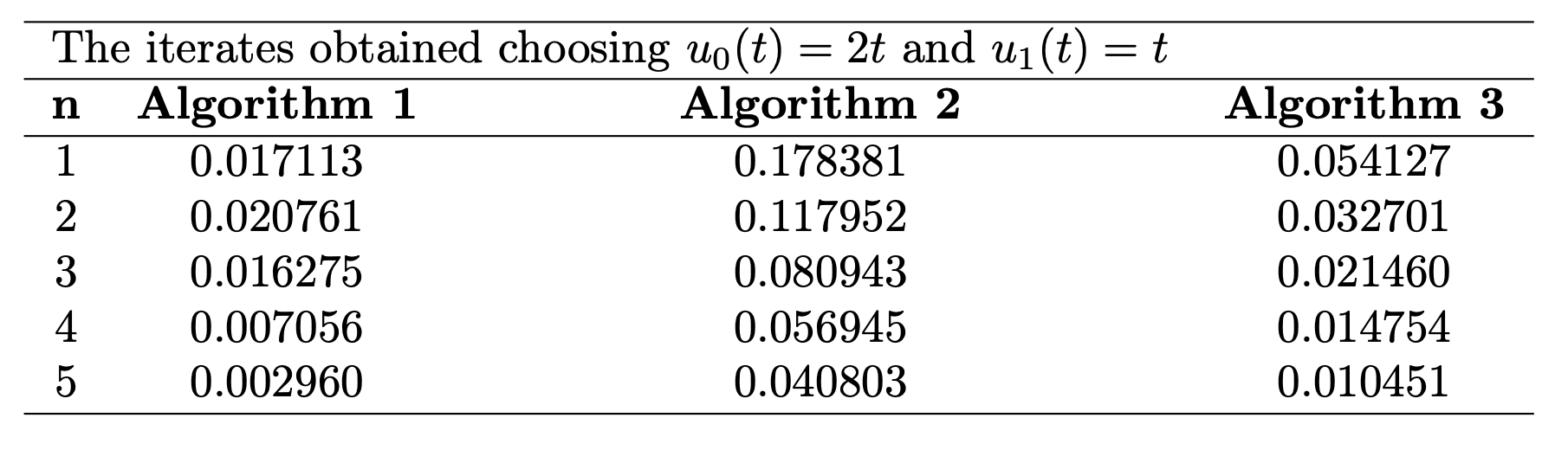
Table 2: Numerical simulations for Example 3
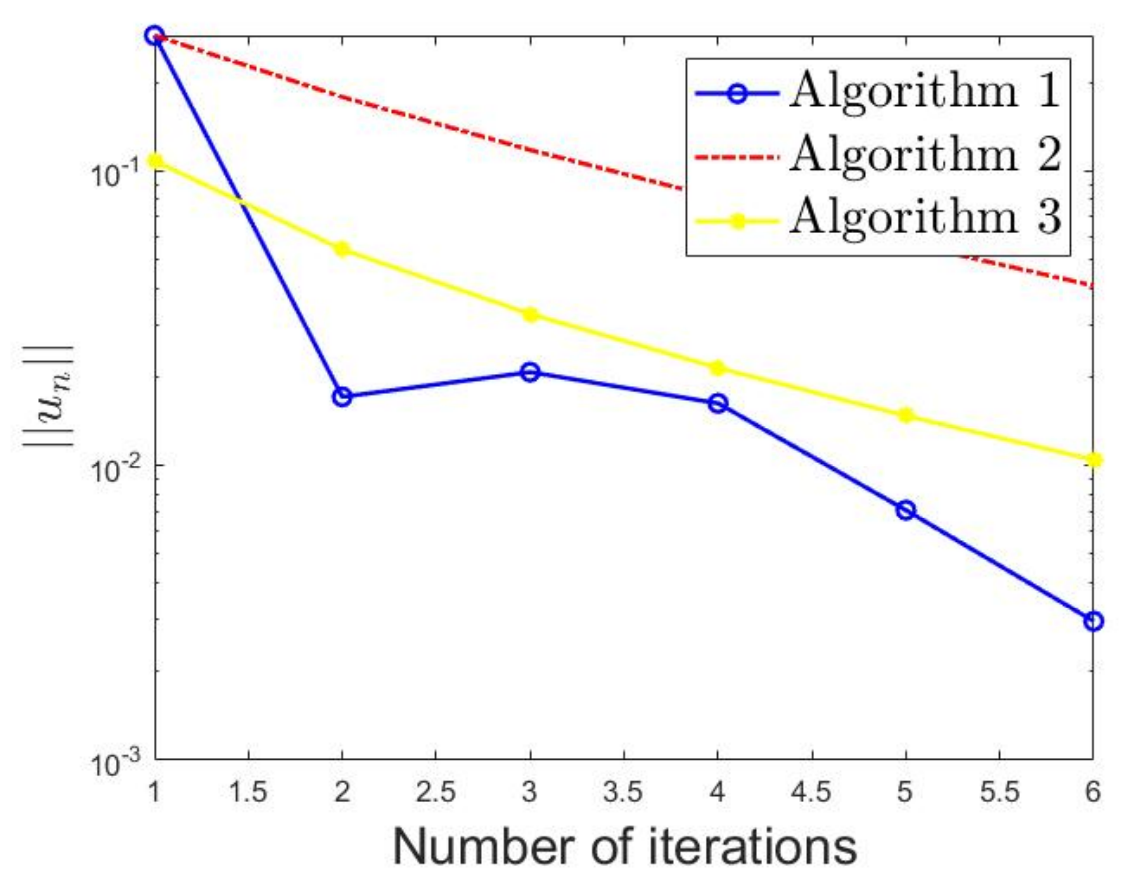
Figure 1. Some iterates of Algorithms 1, Algorithms 2 and Algorithms 3 with initial points x_{0} = 2t and x_{1} = t
5 Future Work
In the next stage of our research, we will extend the relaxed splitting scheme to solve monotone inclusion and fixed point problems without assuming cocoercivity. Our focus is to develop an inertial forward-reflectedbackward algorithm which combines inertial steps, reflection corrections, and adaptive parameters. The proposed algorithm aims to achieve convergence under mild and easy-to-verify conditions.
Algorithm 4
Let \kappa ,\rho \in (0,1) ,\left\{\theta_k\right\} \subset [0,1) and \lambda_k \in \left ( 0, \frac{1}{L} \right ).
1. Given x_0, x_{-1} \in H, compute y_k = x_k + \theta_k(x_k - x_{k-1}).
2. Given y_{k}, compute
v_{k} = (1 - \kappa)y_k + \kappa G\left( (1 - \rho)y_k + \rho G y_k \right).
3. Compute
x_{k+1} = J_{\lambda_k A} \left( x_k - \lambda_k B(v_k) - \lambda_{k-1}(B(v_k) - B(v_{k-1})) \right).
Where A: H \rightarrow H is a maximally monotone operator , B : H \rightarrow H is monotone and Lipschitz continuous, and G: H \rightarrow H is a pseudo-contractive mapping.
Under suitable assumptions on A, B, and the parameters \lambda_k, \theta_k, \beta_k, the sequence {x_k} generated by Algorithm 3 converges weakly to a solution of the monotone inclusion problem.
Theorem 5
In addition, two alternative variants are also under consideration. One of them introduces new reflection-based corrections, while the other modifies parameter updates to suit non-cocoercive operators. These variants are being tested for applications in image reconstruction and signal processing. Early results show that the proposed methods improve both accuracy and computational efficiency.
6 Conclusions

This work studied a forward-backward-forward inertial method for solving variational inclusion and fixed point problems. The main result established that the sequence generated by the proposed method strongly converges to the common solution of the considered problems.
Numerical simulations demonstrated that the combination of relaxation and inertial techniques significantly improves the convergence rate of the proposed method. The quality of images recovered by the proposed method, when compared with the images recovered by existing algorithms, showed that our approach is both efficient and robust in practical applications.
References
This work is part of a broader effort to design robust and adaptive methods for variational problems in convex and non-convex settings.
Read the full paper: K. Kratuloek, P. Kumam, S. Sriwongsa, J. Abubarkar (2024) A relaxed splitting method for solving variational inclusion and fixed point problems, J. Comput. Appl. Math., Vol. 43. No. 70, https://doi.org/10.1007/s40314-023-02583-5
[2] Y. Malitsky (2015) Projected reflected gradient methods for monotone variational inequalities. SIAM Journal on Optimization, Vol. 25, No. 1, pp. 502–520
[3] R. Suparatulatorn, A. Khemphet (2019) Tseng type methods for inclusion and fixed point problems with applications. Mathematics, Vol. 7, No. 12, pp. 1175
|| Go to the Math & Research main page

 Kanokwan Kratuloek
Kanokwan Kratuloek