Flows on Networks
By Enrique Zuazua, Nicola de Nitti
PDE models on Networks
In the last few decades, models based on partial differential equations have been very effective in tackling many applied problems dealing with flows on networks.
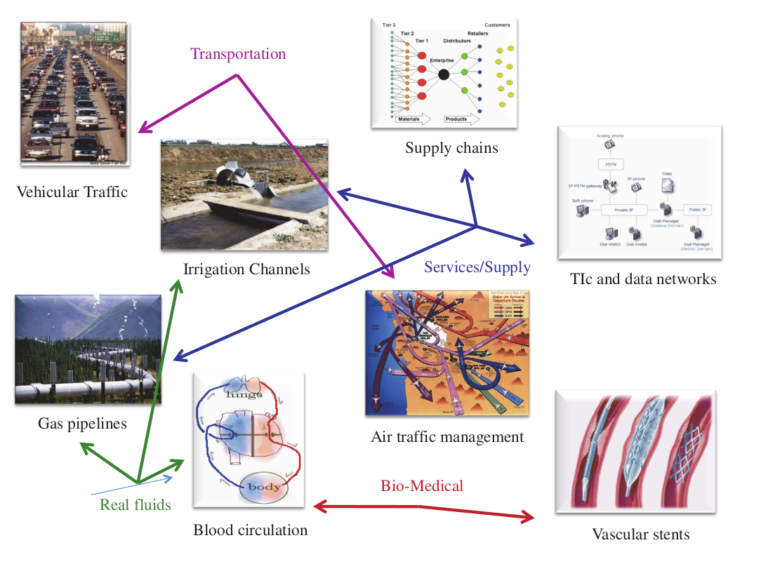
The areas of application include mainly the study of vehicular traffic, supply chains, irrigation channels, gas pipelines, blood circulation, air traffic management, and polymer physics.
Figure 1. Applications of models based on PDEs. Source of the picture: [4, Figure 1, p. 49]
For an overview of the main models and results, we refer the reader to the following surveys and monographs: [4, 12, 11, 10]
A classical example: the LWR traffic flow model
A general network is represented by a directed graph \mathcal G composed by a finite number of edges connected by vertices or junctions. A general mathematical framework for the study of flow problems on a network is given by a system of balance laws in one space dimension
∂t u + ∂x f(u) = g(t,x,u),
coupled with further algebraic conditions imposed on the vertices of the network. For a fixed vertex x_\ast, such conditions can be written compactly as
\Psi(t,u(t,x_\ast+)) = 0.
The physical properties of the system under consideration will induce a specific choice of the function \Psi.
Going forward, we focus on the case of a single node. This is not restrictive because hyperbolic systems have the property that waves propagate with finite speed.
In the study of vehicular traffic, a classical model is the one introduced by Lighthill, Whitham, and Richards (LWR model) in [14, 15]:
∂t \rho + ∂x \left(v_{max}\rho\left(1- \frac{\rho}{\rho_{max}} \right) \right) = 0,
where v_{max} and \rho_{max} denote the (constant) maximum velocity and density of cars respectively. At the junction, we impose the following conditions (following [9]):
• conservation of cars
• traffic distribution (i.e. percentage of drivers coming from the i-th incoming road and turning into the j-th outgoing road)
• flow maximization (i.e. respecting the previous distribution rule, the drivers choose to maximize the flux through the junction)
Here is a simulation of the traffic flow in the case of one incoming roads and two outgoing roads obtained by implementing the Gudonov scheme with MatLab (see [2, 13, 12]).
For further numerical simulations, we refer the reader to [2, 3] and [5, 6]
Our research activities
Sponsored by the Chair of Applied Analysis, Alexander von Humboldt Professorship, we are currently working on several applied problems related to flows on networks:
• Gas pipes modeling (in the framework of the Transregio 154 Project “Mathematical Modelling, Simulation and Optimization using the Example of Gas Networks” of the DFG). We are interested in modeling frictiondominated transportation of isothermal compressible gas through a network of one-dimensional pipes over distances which are significantly larger than diameter of the pipe. Mathematically, we consider a damped isothermal Euler system and we study the well-posedness of global solutions; their longtime asymptotic behavior; and control problems arising in gas distribution
Collaborators: G. M. Coclite (PoliBA), N. De Nitti (FAU), M. Gugat (FAU), E. Zuazua (FAU-AvH)
• Singular limit for conservation laws on networks. The vanishing viscosity approximation of scalar conservation laws on networks has been recently studied in [8, 1, 7]. In this context, we are interested in analyzing more general singular limit problems, where the competing effects of diffusion and oscillations come into play
Collaborators: M. Cavalcante (UFAL), G. M. Coclite (PoliBA), N. De Nitti (FAU), and E. Zuazua (FAU-AvH)
• Vanishing viscosity for systems of conservation laws on networks. While the vanishing viscosity for scalar conservation laws on networks has been intensively studied (see above), analogous problems for many (local and nonlocal) systems modeling traffic flow are still open
Collaborators: G. M. Coclite (PoliBA), N. De Nitti (FAU), A. Keimer (UC Berkeley), M. Garavello (UniMIB), F. Marcellini (UniBS), L. Pflug (FAU), and E. Zuazua (FAU-AvH)
References
[1] B. P. Andreianov, G. M. Coclite, and C. Donadello. Well-posedness for vanishing viscosity solutions of scalar conservation laws on a network. Discrete Contin. Dyn. Syst., 37(11):5913–5942, 2017
[2] B. D. Bergersen. Numerical Solutions of Traffic Flow on Networks: Using the LWR-Model and the Godunov Scheme. Master’s thesis (NTNU Trondheim), 2014. Available at NTNU Open
[3] B. D. Bergersen. Numerical Solutions of Traffic Flow on Networks: Using the LWR-Model and the Godunov Scheme. Master’s thesis (NTNU Trondheim), 2014. Supplementary video material
[4] A. Bressan, S. Cani´c, M. Garavello, M. Herty, and B. Piccoli. Flows on networks: recent results and perspectives. EMS Surv. Math. Sci., 1(1):47–111, 2014
[5] G. Bretti, R. Natalini, and B. Piccoli. Numerical approximations of a traffic flow model on networks. Netw. Heterog. Media, 1(1):57–84, 2006
[6] G. Bretti, R. Natalini, and B. Piccoli. Numerical approximations of a traffic flow model on networks. 2006. Supplementary video material
[7] G. M. Coclite and L. di Ruvo. Vanishing viscosity for traffic on networks with degenerate diffusivity. Mediterr. J. Math., 16(5):Paper No. 110, 21, 2019
[8] G. M. Coclite and M. Garavello. Vanishing viscosity for traffic on networks. SIAM J. Math. Anal., 42(4):1761–1783, 2010
[9] G. M. Coclite, M. Garavello, and B. Piccoli. Traffic flow on a road network. SIAM J. Math. Anal., 36(6):1862–1886, 2005
[10] C. D’Apice, S. Göttlich, M. Herty, and B. Piccoli. Modeling, simulation, and optimization of supply chains. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA 2010. A continuous approach
[11] M. Garavello, K. Han, and B. Piccoli. Models for vehicular traffic on networks, volume 9 of AIMS Series on Applied Mathematics. American Institute of Mathematical Sciences (AIMS), Springfield, MO, 2016
[12] M. Garavello and B. Piccoli. Traffic flow on networks. Conservation laws models, volume 1 of AIMS Series on Applied Mathematics. American Institute of Mathematical Sciences (AIMS), Springfield, MO, 2006
[13] R. J. LeVeque. Numerical methods for conservation laws. Lectures in Mathematics ETH Zürich. Birkh¨auser Verlag, Basel, second edition, 1992
[14] M. J. Lighthill and G. B. Whitham. On kinematic waves. II. A theory of traffic flow on long crowded roads. Proc. Roy. Soc. London Ser. A, 229:317–345, 1955
[15] P. I. Richards. Shock waves on the highway. Operations Res., 4:42–51, 1956
|| Go to the Math & Research main page