Federated Learning: Protect your data and privacy
Federated Learning is becoming an increasingly popular topic in machine learning. But what is it, and why do we need it? To explain what the excitement is all about, this post outlines the basics of Federated Learning and the mathematical principles behind it.
Federated Learning: what and why?
Pioneered by Google [1], Federated Learning was created to train machine learning models on large, distributed datasets without sharing the data with a central server. This is useful for a number of reasons. First, moving large amounts of data requires time and, as we all know very well, time is money. Second, the training data may be simply too large to be collected and stored in a central location. Finally, and perhaps most importantly, data could be too sensitive to be shared.
An illuminating example comes from healthcare. Good machine learning models have enormous potential to improve patient diagnosis and treatment, but patient data collected by a hospital is often protected by privacy policies that prevent it from being shared. In this situation, Federated Learning can enable one to train a machine learning model using data from multiple hospitals without breaking privacy laws [2]. Federated Learning also holds tremendous potential to advance the “internet of things”: one can train speech recognition models in real-time on individual wearable devices without sharing potentially sensitive audio data [3], or learn to control a fleet of autonomous cars with minimal communication between them [4].
The mathematical formulation
As in every machine learning framework, Federated Learning aims to determine a vector w of model parameters that minimize a loss function F(w). This loss function is usually the average of individual loss functions F_1(w), \ldots, F_n(w) that evaluate how well the model performs on a set of n training data points for a given choice of parameters. Thus, the problem is stated mathematically as
\min _w \frac{1}{n} \sum_{i=1}^n F_i(w) .
When the training dataset consists of inputs x_1, \ldots, x_n to be classified (e.g., images of animals) and corresponding classification labels y_1, \ldots, y_n (e.g., “cat”, “dog”, “elephant”), one usually takes the ith loss function F_i(w) to be the error between the exact and predicted labels of the ith data point.
The difference between traditional machine learning and Federated Learning is that the dataset is distributed among a number K of different clients (or devices). Each client owns a number n_k of data points, which may differ from client to client. Combining terms owned by each client, the training problem can be rewritten as
\min _w \sum_{k=1}^K \frac{n_k}{n} f_k(w)
where
f_k(w):=\frac{1}{n_k} \sum_{i \in \text { client } k} F_i(w)
is the average loss of each client. The goal of Federated Learning is to solve this optimization problem without exchanging data between agents.
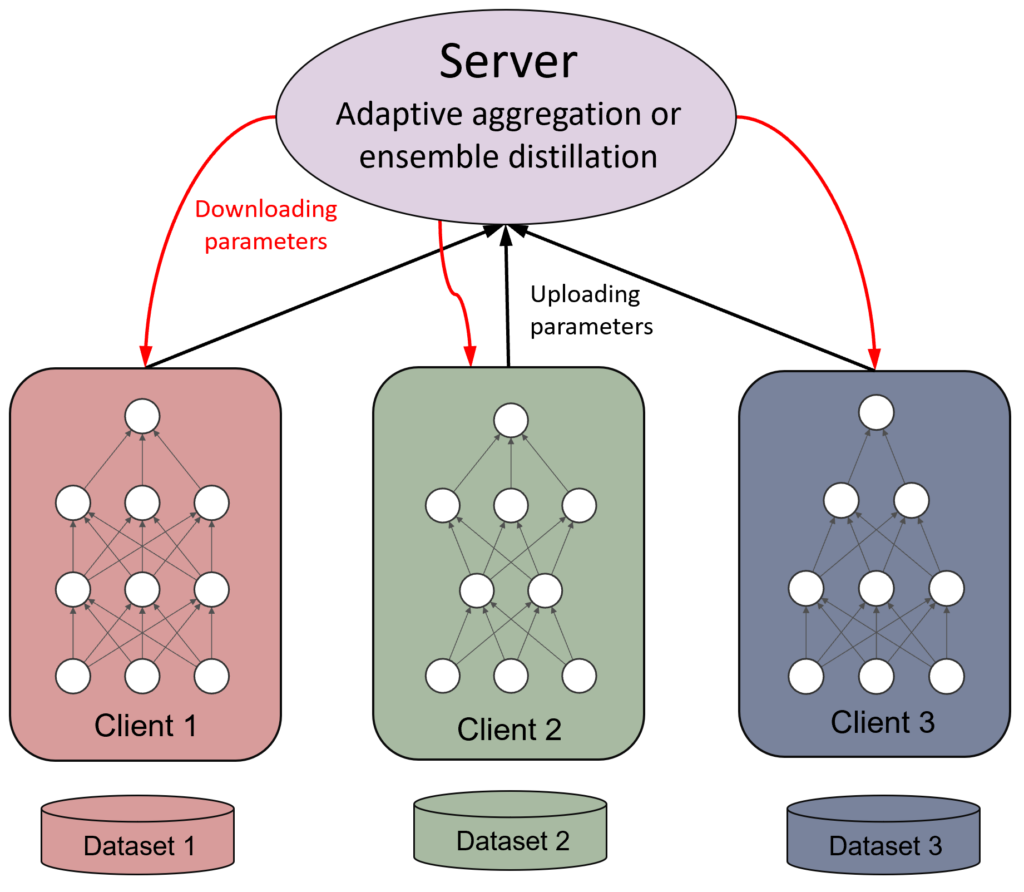
Figure 1. A schematic illustration of a Federated Learning architecture.
The training process
A common Federated Learning algorithm achieves data privacy by combining local parameter updates on each client with “model aggregation” steps performed by a central server. Figure 1 illustrates the situation: each client uses its own data to propose values for the model parameters, and the central server tries to enforce a consensus between the individual client proposals. A simple strategy to achieve this proceeds as follows:
1. Initialization: The server initializes model parameters to begin the training.
2. Client selection: The server selects a subset of clients for a training round.
3. Server broadcast: The server distributes the model to the selected clients.
4. Client update: Each selected client trains the model on its own data.
5. Server aggregation: The model parameters obtained by each client are sent to the server, where they are averaged.
The process is then repeated for several round of training, starting each time from the averaged model parameters obtained at step 5. This leads to the Federated Averaging (FedAvg) algorithm from [1]:
Algorithm 1. Federated Averaging
Initialize model parameters w_0 on server
for each training round t=1,2, \ldots, T do
S_t \leftarrow (random set of M \leq K clients)
for each client k \in S_t in parallel do
w_{t+1}^k \leftarrow ClientUpdate \left(k, w_t\right)
end for
w_{t+1} \leftarrow \sum_{k=1}^K \frac{n_k}{n} w_{t+1}^k
end for
Of course, in practice one needs to specify how each client update at step 4 works. Typically, this is done by performing E steps of gradient descent with some learning rate \eta (also known as the step size). Algorithmically, this takes the following form:
Algorithm 2. Client Update
ClientUpdate (k, w):
for local epoch i=1,2, \ldots, E do
w \leftarrow w-\eta \nabla F(w)
end for
return w to server
Federated Learning in action
Now that we understand how Federated Learning works, let us see how it performs. We applied the FedAvg algorithm of [1] discussed above to a handwriting recognition problem from the MNIST database [5], which contains images of handwritten digits. We used 60,000 images for training and 10,000 images for model validation.
The parameters of our implementation are:
• K=100 clients
• M=10 clients selected for each training round
• E=5 steps of gradient descent in each client update step
• Learning rate \eta =0.01.
We also consider six different model architectures:
• FedAvg-MLP1: One hidden layer with 200 units and ReLU activation functions.
• FedAvg-MLP2: Two hidden layers with 200 units each and uses ReLU activation functions.
• FedAvg-CNN1: Two 5\times5 convolution layers with 5 and 10 channels, respectively. Each layer is followed by a 2\times2 max pooling, a fully connected layer with 50 units and ReLU activation functions, and a final softmax output layer.
• FedAvg-CNN2: Two 5\times5 convolution layers with 32 and 64 channels, respectively. Each layer is followed by a 2\times2 max pooling, a fully connected layer with 512 units and ReLU activation functions, and a final softmax output layer.
• FedAvg-ResNet1: Two residual blocks, each block containing two convolution layers with the same number of channels and kernel size as those in FedAvg-CNN1.
• FedAvg-ResNet2: Two residual blocks, each block containing two convolution layers with the same number of channels and kernel size as those in FedAvg-CNN2.
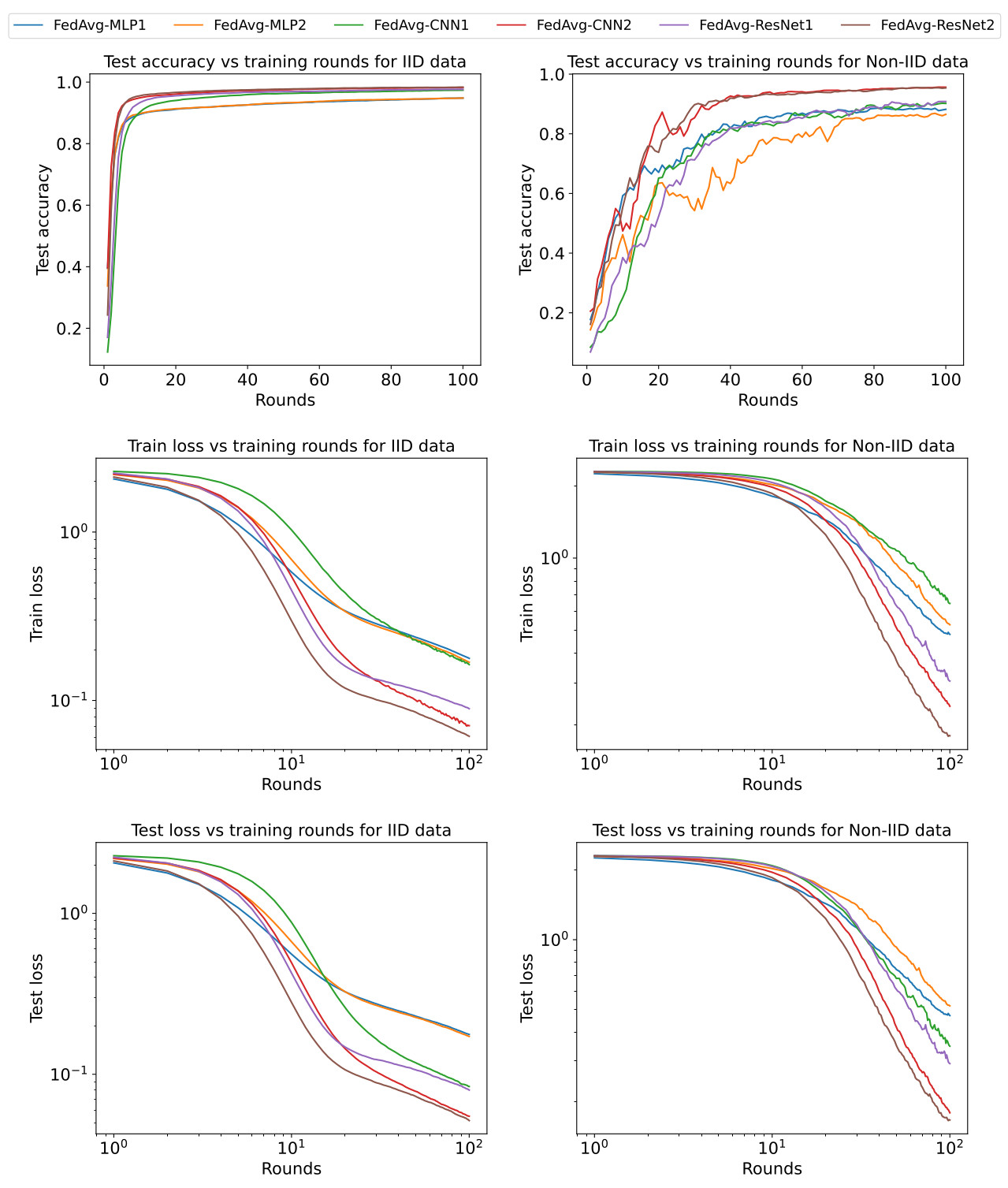
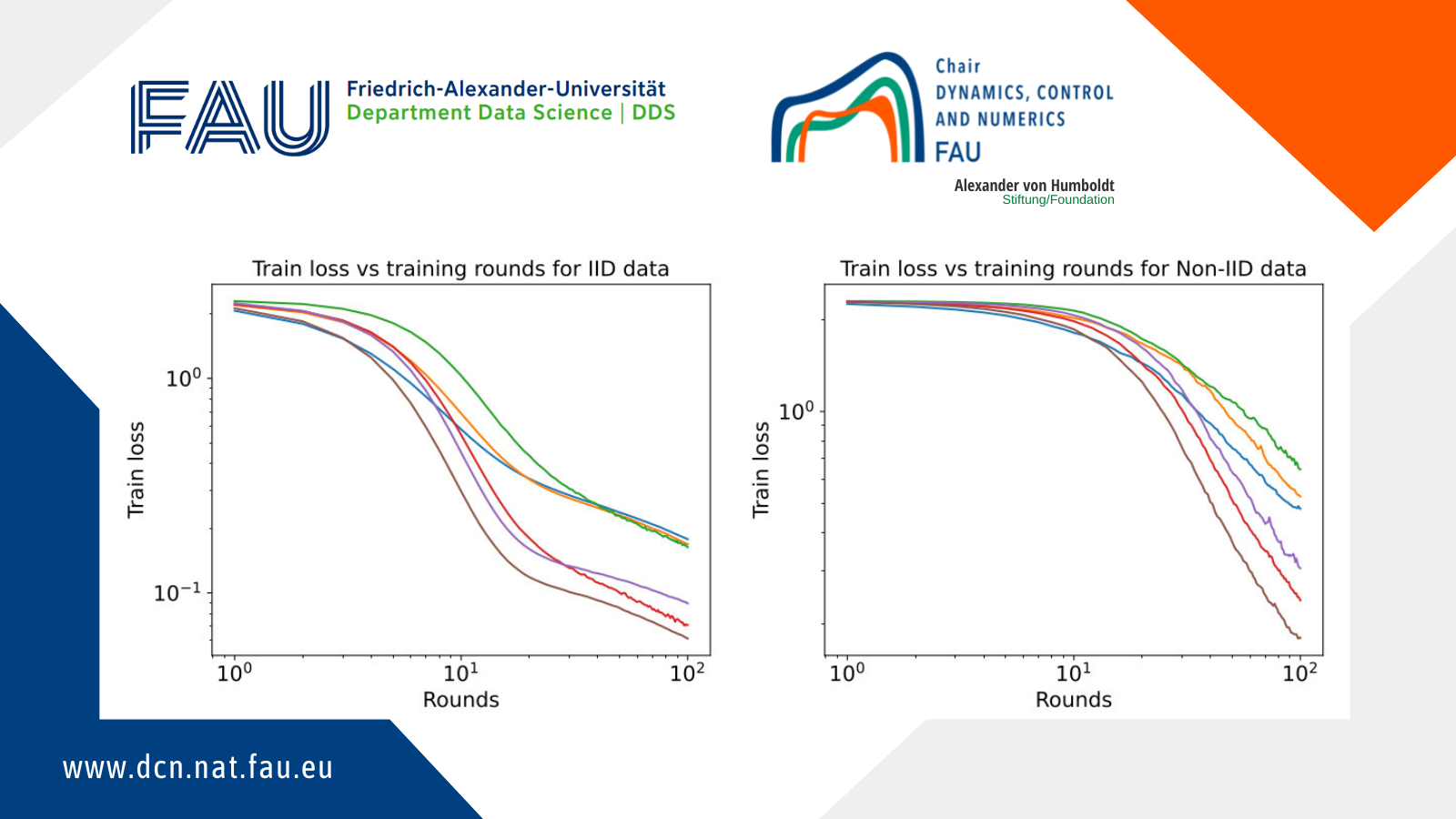
Figure 2. Test results for the experiments we conducted; see the test for a description of model architecture and algorithm parameters.
Finally, for each model architecture we consider two test cases. The first assigns equal amount of data to each client in an independent and identically distributed (IID) way. In the second test case, instead, the data is assigned in a non-IID way by sorting the database, dividing it into 200 groups of 300 images, and assigning two groups to each client. This means each client only has one or two digits in their data.
The test results are shown in Figure 2 for both test cases and all model architectures. In all cases, the training loss decreases with the number of training rounds, while the predictive accuracy on the test set of 10,000 images not used for training increases. For the IID data case, after 100 training rounds all models successfully identify at least 94% of the test images. In particular, the FedAvg-CNN and FedAvg-ResNet models have a success rate of more than 98%. For the non-IID data, results are similar but the training process is slower and more oscillatory. This time, all models have a success rate of at least 86% after 100 rounds of training, which rises to 95% for the FedAvg-CNN and FedAvg-ResNet models.
What comes next?
The test results above demonstrate that Federated Learning promises to be a powerful method to train machine learning models on privacy-protected datasets. This is of paramount importance in a world where user privacy is becoming an increasingly strongly felt issue.
However, there are a number of challenges remaining to be solved. One is the potential presence of uncooperative clients, which would spoil the performance of the consensus-seeking algorithm we have described. Another challenge is to train a machine learning model from heterogeneous clients, each of which learns a private model that needs not be of the same type as that of other clients. This makes it impossible to simply average the clients’ models, requiring more sophisticated consensus strategies. Our research group is currently working to overcome some of these challenges.
References
[1] Brendan McMahan, Eider Moore, Daniel Ramage, Seth Hampson, and Blaise Aguera y Arcas. Communication-efficient learning of deep networks from decentralized data. In Artificial intelligence and statistics, pages 1273–1282. PMLR, 2017.
[2] Theodora S Brisimi, Ruidi Chen, Theofanie Mela, Alex Olshevsky, Ioannis Ch Paschalidis, and Wei Shi. Federated learning of predictive models from federated electronic health records. International journal of medical informatics, 112:59– 67, 2018.
[3] Jie Xu, Benjamin S Glicksberg, Chang Su, Peter Walker, Jiang Bian, and Fei Wang. Federated learning for healthcare informatics. Journal of Healthcare Informatics Research, 5(1):1–19, 2021.
[4] Tengchan Zeng, Omid Semiariy, Mingzhe Chen, Walid Saad, and Mehdi Bennis. Federated learning on the road autonomous controller design for connected and autonomous vehicles. IEEE Transactions on Wireless Communications, 2022.
[5] Y. Lecun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
|| Go to the Math & Research main page