Felix Klein: A Legacy of Innovation in Mathematics and Education
By Roberto Rodríguez del Río, Complutense University of Madrid | IES San Mateo, Madrid
Felix Christian Klein lived in a period of history of science in which Mathematics were involved in a process of transformation, leaving behind the classical and individualist vision of Newton, Leibniz and Gauss. One of his most important contributions, the Erlangen Program, led to a new vision of Geometry. Klein left, also, an important legacy that set basis for innovation and improvement of teaching Mathematics.
Felix Klein was born on April, 25, 1849 or like he liked to say 2^2, 5^2, 43^2 . He lived in an amazing period of history of science in which Mathematics, and Science in general, were involved in a process of transformation. During that time, for example, two of the more relevant theories of Physics were developed: Relativity and Quantum Mechanics. In that time, “On the Origin of Species” by Charles Darwin were published. The Science were changing the way we see the World. Mathematics were also involved in an important process of transformation, leaving behind the classical and individualist vision of Newton, Galileo, Leibniz or Karl Gauss.
The Language of the Symmetry
One of the ideas that has fascinated to Mathematicians is Symmetry. Symmetry surrounds us. Wherever we look, we find symmetry. So, what is Symmetry? And how can we talk about Symmetry? We also need to establish a mathematical language to talk about Symmetry.

Fig. 1: Mosaic, La Alhambra
It is common to find the words Symmetry and Beauty in the same sentence. Mosaics in La Alhambra, in Granada, Spain are one of the examples in which, both concepts, Symmetry and Beauty, are masterfully combined. The ancient Muslim artists who decorated the Alhambra were not allowed to represent human figures. So they found in Geometry and Symmetry a way to express beauty. When we look at the mosaics of the Alhambra, words like repetition, pattern, measure, proportion, order and, obviously, beauty.
Like so many other fundamental mathematical ideas, defining Symmetry is not easy. And sometimes the best definition is the simplest one. Herman Weyl wrote in his book “Symmetry” what is, without a doubt, one of the best definitions of Symmetry:
“A thing is symmetrical if there is something you can do to it, so that, after you have finished doing it; it looks the same as before.” It is exactly the idea that we get when we study mathematical concepts such as bilateral or axial symmetry, radial symmetry, or spherical symmetry.

Once we have settled one definition of Symmetry, we need a language to be able to talk about it. And that language, that mathematical language, is Group Theory. Take a square ABCD and let’s consider the transformations (rotations in this case), that leave fixed, that leave the same, the square ABCD.
The set of 4 elements G = { e, p, q, r } is what mathematicians call a Group. Not only the 4 elements but The operation that involves applying two of the rotations one after the other.
The word Group was first used by the French mathematician Évariste Galois (1811-1832). Galois introduced the idea of a Group to solve the general problem of expressing the solutions of an algebraic equation by means of radicals. As for example the formula to solve the equation of the second degree a x^2 + b x + c = 0, that is  We can solve, by means of a formula with radicals, the equations of the second, third and fourth degree, but for the particular case of the fifth degree equation, the Norwegian mathematician Niels Henrik Abel (1802-1829) had proved that it was impossible to find a general solution with radicals.
We can solve, by means of a formula with radicals, the equations of the second, third and fourth degree, but for the particular case of the fifth degree equation, the Norwegian mathematician Niels Henrik Abel (1802-1829) had proved that it was impossible to find a general solution with radicals.
Évariste Galois died in tragic circumstances, in a duel, in Paris. But it was in Paris that the new Group Theory was being developed. In the second half of the 19th century, if you wanted to learn about the new Group Theory, you necessarily had to travel to Paris. And that was what Felix Klein did, travel to Paris. He was 21 years old when, in 1870, he was in Paris with his friend the Norwegian mathematician Sophus Lie (1842-1899). They were in Paris working with Camille Jordan (1838-1922), and they were in Paris precisely to study Group theory, developed by Galois. Felix Klein, probably, did not think at the time he was going to become responsible for a new revolutionary vision of Geometry. But, very soon, he realized that Geometry, the idea of Symmetry and Group theory were strongly related.

Unfortunately for Klein and Lie the travel had to end much earlier than planned. The Franco-Prussian War was declared on July, the 19th, in 1870. Klein was Prussian, so he immediately went to Berlin. But, his friend Sophus Lie thought that the War was not his business because he was a Norwegian. The problem was that for a french policeman it is not so clear, especially in times of War. For the French Police Sophus Lie was a strange young man that was able to speak German and he carried in his bag sheets written with lots of strange symbols, which seemed to be encrypted messages. As a result, Lie was arrested. He spent one month in prison. He was released from prison after a month, thanks to the intervention of the French mathematician Gaston Darboux (1842-1917) and probably Camille Jordan, and finally he was able to travel to Norway.
Before going to Paris, Felix Klein and Sophus Lie met in Berlin. Klein had studied at the Universities of Bonn and Göttingen and went to Berlin to attend classes with Karl Weierstraß (1815-1897). Klein’s stay in Berlin was very fruitful, because he met other young mathematicians, such as Lie, but he was not very friendly with Karl Weierstraß.
Karl Weierstraß, perhaps the most important german mathematician at that time, had a very different way of understanding mathematics from Klein’s way. Weierstraß was a rigorous and formalist mathematician, and did not share the intuitive form of Klein, who used graphs and physical ideas in his classes, something that Weierstraß strongly disapproved.
The Erlangen Program
Let’s have a look at the situation of the Geometry in the second half of 19th century. A situation that led Klein to develop his famous program.
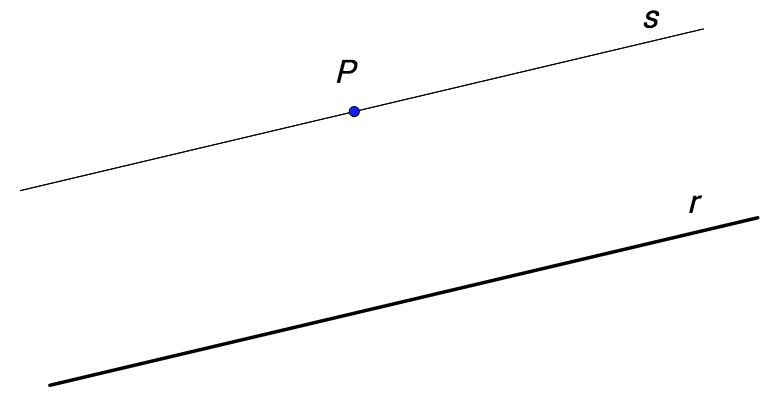
For two millennia the only source of Geometry had been The Euclid’s Elements. The fifth Postulate of the Element’s or its equivalent, the Parallel Postulate, is the key of the Euclidean Geometry. The Parallel Postulate says: “Given any straight line and a point not on it, there exists one and only one straight line which passes through that point and never intersects the first line”. If we admit that there exists more than one, or if we admit that there is no one, without no logical contradictions, we can construct Non-euclidean Geometry. These ideas, which led to the invention of non-Euclidean geometries, were carried out, mainly, by Karl Friedrich Gauß (1777-1855), János Bolyai (1802-1860), Nikolái Lobachevski (1792-1856) and Bernhard Riemann (1826-1866).
Let’s go back with Felix Klein. After returning from France, Felix Klein enlisted in the army, but he contracted typhus, so he had to leave it. He got a Privatdozen position at the University of Göttingen. And he published two papers on Non-Euclidean Geometry, one in 1871, and the another one in 1873, Über die sogenannte Nicht-Euklidische Geometrie, Mathematische Annalen, On the so-called non-Euclidean geometry. In these works he proved that Euclidean and Non-Euclidean geometry could be considered particular cases of projective geometry, but most importantly, he built models for the new geometries.

To find euclidean models for Non-euclidean geometries was an important matter. For the followers of the philosopher Immanuel Kant (1724-1804) it is only possible to imagine Euclidean geometry. Therefore, the construction of these models was a kind of justification before the Philosophers. And this is, probably, the reason of the title of the paper of Klein: On the so-called non-Euclidean geometry.
Thanks in part to these papers, Felix Klein got a position as a Full Professor in Erlangen, at 23 years old. As a new Professor, he was required to give an inaugural lecture. In his lecture he spoke mainly about the importance of cultivating applied mathematics together with pure mathematics, in order to connect different fields of knowledge, such as physics or technology. He also spoke about the importance of imagination and intuition for mathematics and about his plans to organize talks and seminars. But actually what has gone down in history is the manuscript that he later presented: The so-called Erlangen Program. The original title of the Erlangen Program was: A comparative review of recent researches in geometry. Before the Erlangen Program, mathematicians understood geometry in terms of objects: points, lines, circles, and the relationships between them: distances, angles. Klein’s point of view is different. He suggested that geometry itself was not characterized by objects but by the Group of transformations that preserve certain properties, such as distances or angles, for example. The Erlangen Program (E.P.) is not a research paper. It is a non technical presentation, even philosophical, of the ideas that Klein had discussed with Sophus Lie, whose collaboration was essential for the composition of the Program. The Erlangen Program is the culmination and synthesis of many previous mathematical studies and is not the work of a single author. As Klein himself later recognized, many of the ideas were due to his friend Sophus Lie. At the beginning, the Program did not receive much attention. Maybe some of the reasons because this is so, are that some mathematicians of Berlin considered Klein, in their own words, “A charlatan without real merit.” Anyway, in 1880, versions in Italian, French and English appeared.
While in Erlangen Felix Klein became Editor of the Mathematische Annalen, a position which he held almost to the end of his life. And he managed to make the Journal the most prestigious of his time. In 1875, Felix Klein left Erlangen. He was in Erlangen for only 3 years. Why? Maybe it’s because he didn’t have many students or maybe the only reason is that he was very young. He was 25 years old. The true is that when Felix Klein left Erlangen, he was an internationally recognized mathematician. He went to Munich and, later, to Leipzig. Let’s see some more innovations due to Felix Klein.
The Klein’s bottle and Henri Poincaré
It is believed that the first person to think that the Earth has a spherical shape was Pythagoras (c. 570-c. 495 BC), although there is no evidence. We do know for sure that Aristotle (384-322 BC) thought so, and even that Eratosthenes (276-194 BC) was able to measure the circumference of the Earth by an ingenious procedure. Anyway, we understand that the ancients —or even children— thought that the Earth was flat. The reason is that if small distances are considered, the spherical surface appears flat.
In 1882, Felix Klein had an idea by modifying and changing the previous argument. In fact, he showed that any surface can be represented by a portion of a flat polygon. So, in this way, we can represent a torus by means of a rectangle, identifying points on opposite sides.
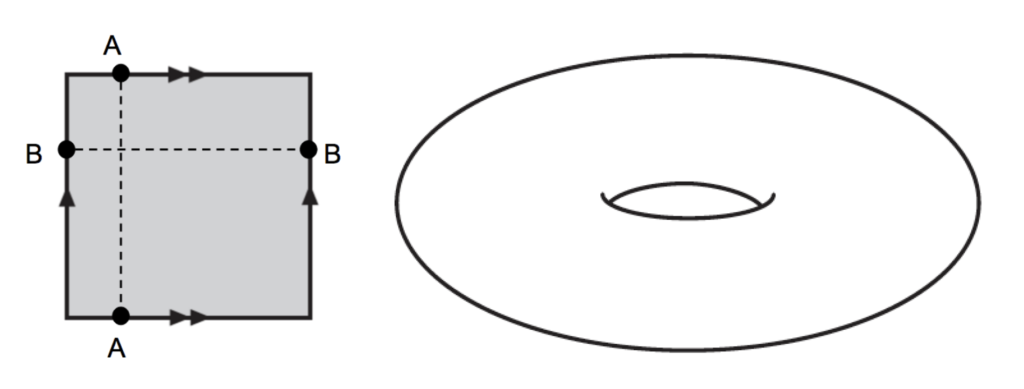
If we only identify, inverting them, the points of two of the sides of the rectangle, we obtain a Möbius strip.
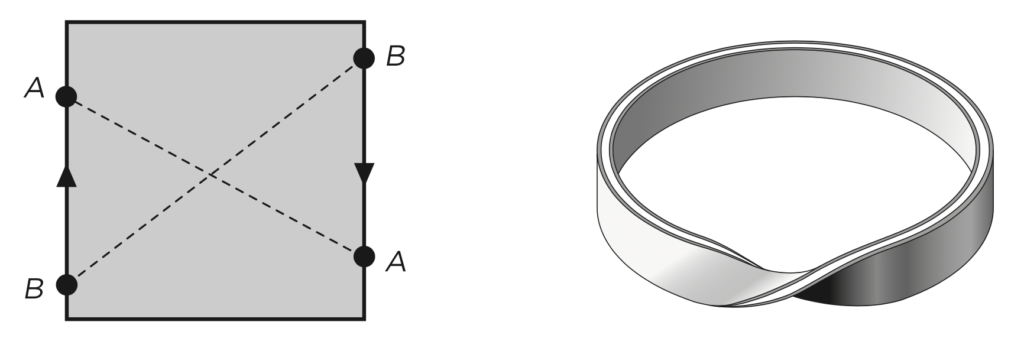
But, if in the previous square, that of the Möbius strip, we also identify —glue— the points of the other two sides, then we obtain the Klein bottle, probably one of the most famous surfaces in mathematics. We can see that the Klein bottle as two Möbius strips together. The part of mathematics that studies these surfaces is what we call Topology. Despite the fact that Topology is considered today as an independent branch of mathematics, its definition fell within the category of Geometry, according to the Erlangen program of Felix Klein. Indeed, Topology can be considered as the study of the properties of the surfaces that remain invariant under the action of the Group of homeomorphisms. Homeomorphisms are a type of transformation that “deforms” surfaces without breaking them, as if they were made of rubber.
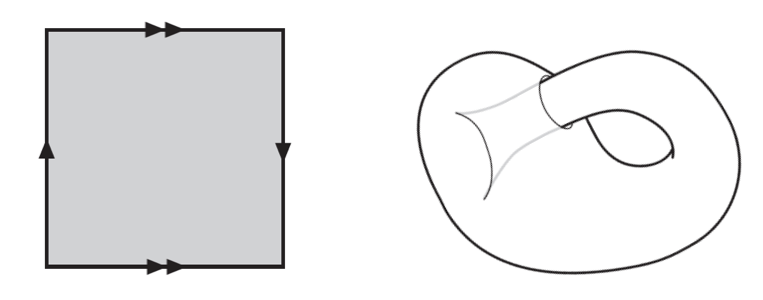
Although this object was originally called “Klein surface”, a translator mistook the German words Fläche und Flasche, and he translated “Klein Bottle”. From a marketing point of view, it was a success, so choosing a good name, even in math, is very important.
One of Felix Klein’s research topics was automorphic functions, which are a type of special complex functions. The French mathematician Henri Poincaré (1854-1912), also worked on automorphic functions. He also worked on non-Euclidean geometries. Poincaré, who became one of the most original and imaginative mathematicians in the history of mathematics, was four years younger than Klein. He was an unknown mathematician while Klein was well-renowned. However, he made very rapid advances and between them, Poincaré and Klein, a strong competition arose to achieve more and better results. It must be said that the competition was won by Poincaré and this fact led Klein to a severe depression from which it took him a long time to recover. Many years later, Klein said that this episode caused him to never regain his productivity. Fortunately, he recovered and, as we will see, he continued to be very productive.
Göttingen: «The Mecca of mathematicians»
While Klein was ill, he received an offer to go to work at John Hopkins University in Baltimore. In Baltimore was the English mathematician, James Joseph Sylvester (1814-1897), but in 1883 he left his post to return to England and he suggested the name of Felix Klein to replace him. However, the University of Baltimore did not accept Klein’s economic conditions. But in 1886, Felix Klein received an offer to occupy a Professorship at Göttingen University. And he accepted immediately. In this case, the money was not a problem.
Probably, the reason why Klein immediately accepted the offer was the rich mathematical tradition of Göttingen. A Tradition that started with Gauß and some of his most prominent students, such as Sophie Germain (1776-1831), Richard Dedekind (1831-1916), Bernard Riemann (1826-1866).

The University of Göttingen was one of the first to incorporate, in a very complicated way at first, women into the world of research. In addition to Sophie Germain, Sofia Kovalevskaya (1850-1891) also obtained her Ph.D. in Göttingen, thanks to the three scientific reports that she presented, and with the help of Karl Weierstraß. Grace Chisholm Young (1868-1944), an english student that obtained her Ph.D. with Felix Klein as her advisor. Emmy Noether (1882-1935), one of the leading modern mathematicians, came to Göttingen in 1915 to work with Klein and David Hilbert (1862-1943) on problems in Relativity Theory. She stayed until 1933, when she was one of the first to lose her position under the new National Socialist regime. Emmy Noether was born and educated in Erlangen. Her father, Max Noether, was a professor of mathematics at the University of Erlangen.
Along with Klein, one of the mathematicians who did the most for Emmy Noether to work in Göttingen was David Hilbert. When Klein took over the leadership of the Göttingen Institute of Mathematics, it was clear to him that one of the keys for Göttingen to become a research world reference center was to create a world-class team. And his first steps consisted in bringing mathematicians as David Hilbert and Hermann Minkowski (1864-1909) to Göttingen. (Both, Hilbert and Minkowski worked at the University of Kögnisberg). The Nobel laureate in physics, Max Born (1882-1970), said that Göttingen had become the Mecca of mathematicians and Klein, Minkowski and Hilbert were his prophets.
David Hilbert was “the man of the future”, said Klein. Klein was the organizer and Hilbert was the problem solver. David Hilbert was commissioned to represent Göttingen at the World Congress of Mathematicians in Paris (1900), where he directed his famous conference on the Problems that would mark the development of mathematical research during the 20th century.
In 1933 when the Nazis took over Germany, many Jews, as Emmy Noether, were “forced to leave”, as they said. As a gesture of defiance, Hilbert never lectured at Göttingen again. Felix Klein retired in 1913, although he continued to work with Hilbert in general relativity. He passed away on June 22, 1925. After Klein, Göttingen continued to be a very active center for research, thanks in part to Klein’s work, until its decline began in 1933.
The Legacy of Felix Klein in Teaching Mathematics
It is not very common for great scientists to worry about teaching. But from 1900 on, Felix Klein became interested in the instruction of elementary mathematics. He was involved and led lots of projects to reform mathematics education and ended up having a huge influence in the teaching of mathematics, which continues in our days.
The Klein Project is a project of IMU/ICMI (this commission was founded by Felix Klein). This Project began in 2008, with the aim of producing mathematics resources for secondary teachers on contemporary mathematics. It was inspired by Felix Klein’s book “Elementary Mathematics from a Higher Standpoint”, first published 100 years earlier. A design group was established, and plans formed to produce articles, web pages, international meetings, and, a Book, like the one that was written by Felix Klein, with contemporary mathematics accesible to mathematics teachers. There is a website, a blog, there are some very interesting materials and some international conferences are held, although perhaps these materials are very little known by secondary school teachers, and we can read in the web of the Project that “In 2016, the Klein group decided to abandon the original task of writing a Klein Project book, and just focus on the blog and/or webpage.”
Felix Klein had strong scientific convictions and there is no doubt that he was a leader. He was able to put Göttingen at the forefront of research and also managed to implement a major project that, more than 100 years later, we can continue to enjoy. Felix Klein believed that the best way to improve the teaching of mathematics was to improve the mathematical training of teachers at pre-university levels, the teachers of the Gymmasium. To achieve this, he got down to work, and developed and taught a series of courses for these teachers, the fruit of which was this famous book, translated into almost all languages: “Elementary Mathematics from a Higher Standpoint” (This last edition by Springer-Verlag was made very recently). Thanks to Felix Klein, high school students study the concept of function, and they study the fundamentals of differential and integral calculus, for example.
Felix Klein thought that it was very important for a teacher to have a knowledge of the historical development of mathematics and that we, teachers, have to be very cautious when introducing the abstraction into mathematics. These words were written more than 100 years ago:
The child cannot possibly understand if numbers are explained axiomatically as abstract things devoid of meaning, with which one can operate according to formal rules. On the contrary, he associates numbers with concrete representations. They are nothing else than quantities of nuts, apples, and other good things, and in the beginning they can be and should be put before him only in such tangible form. […] Mathematics should be associated with everything that is seriously interesting to a person at the particular stage of his development. Elementary Mathematics from a Higher Standpoint.
This article is an extract of our recent book on the life and mathematical contributions of Felix Klein:

Book versions available:
–French: R. RODRÍGUEZ DEL RÍO. Une nouvelle conception de la géométrie. Felix Klein. Colección Génies des Mathématiques. RBA, Le Monde-L’Obs, Francia-Bélgica, 2018
–Italian: R. RODRÍGUEZ DEL RÍO. Una nuova visione della geometria. Klein. Colección Geni della Matematica, RBA, Italia, 2017
References
–F. Klein, A comparative review of recent researches in Geometry, (Complete English Translation). arXiv:2008.02491
-F. Klein, Elementary Mathematics from a Higher Standpoint, Springer, 2016.
-M. Livio, The Equation That Couldn’t Be Solved, Simon & Schuster, 2005.
-R. Rodríguez del Río, Felix Klein. Una nueva visión de la geometría, RBA, Barcelona, 2017. (Felix Klein. A New Vision of the Geometry. Version in Italian and French are available).
-R. Tobies, Visions for Mathematics, Applications, and Education, Birkhäuser, 2021.
–The Klein Project
|| Go to the Math & Research main page
You might like!
Slides available from the FAU-DCN Seminar by Prof. Roberto Rodríguez del Río | April 14, 2021
|| Go to the Math & Research main page