Neural networks and Machine Learning
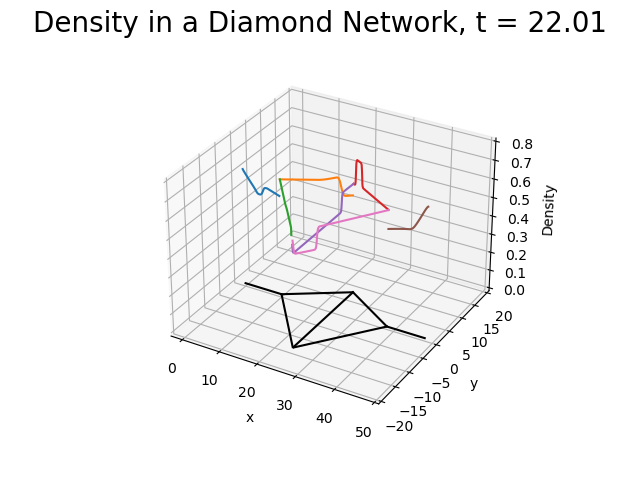
Neural Networks with time delayed connections
Neurons communicate with each other through electrical signals. It is well known that these signals are oscillatory and that the properties of the oscillations depend on the characteristics of the individual neurons, how the neurons are connected, and the presence of time delays in the connections.
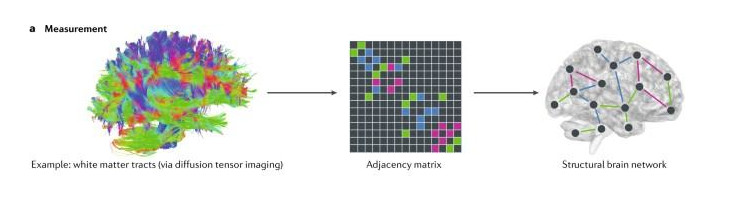
Why do neural cells in different brain structures have different characteristics? Why are neural cells connected in some ways and not others? How do time delays affect the answers to these questions?
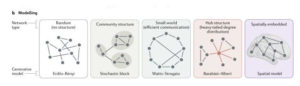
Computational Neurosciences, AI and Machine Learning
Cognitive systems theory is located at the crossroad between Computational Neurosciences and Machine Learning, as it regards both biological and Artificial Intelligence (AI). Neuroscience provides two advantages for AI. First, Neuroscience provides a rich source of inspiration for new types of learning algorithms, independently of mathematical techniques that have dominated traditional approaches in AI, such as neural networks and deep learning. Secondly, neuroscience can provide validation of AI techniques that already exist and those that would be newly developed. If an AI learning algorithm is subsequently found to be implemented in a real biological brain, then that could be a powerful support for it to be an integral component of a general intelligent artificial system.
On the other hand, AI techniques could benefit neuroscience in a feedback fashion. That is, AI and mainly machine learning algorithm has already and continues to transform neuroscience by providing very efficient tools to analyze neurophysiological data.

My interests in this new area of my research are still in their infancy. But with a deep understanding of the research questions addressed in other areas of my research, I am ready to tackle new research questions in intelligent systems and biomedical engineering. My first long-term goal is to formulate generating principles allowing to construct modular information processing cognitive systems that are, as far as possible, self-organizing. My interest here involves both autonomous systems with self-sustained neural activity and self-organized locomotion based on the theories and working principles for neural models and synaptic learning.
My second interest is the use of Machine Learning techniques to analyze neurophysiological data, such as MRI, EEG, and MEG from patients with neurodegenerative diseases (Epilepsy, Alzheimer’s, and Parkinson’s diseases), make diagnose out of this big-data, and then possibly develop new therapies (only in terms of control via deep brain stimulation to control synchronization, mostly responsible for these chronic diseases).
My approach is based on mathematical analysis (chiefly using nonlinear dynamical systems theory and probability theory), numerical simulations, and very recently, neurophysiological data analysis via machine learning techniques. I am also very enthusiastic to collaborate with experimental neuroscientists, biomedical engineers, and neurologists!
References
- Marius E. Yamakou, Poul G. Hjorth, Erik A. Martens: Optimal self-induced stochastic resonance in multiplex neural networks: electrical vs. chemical synapses. Frontiers in Computational Neuroscience 14, 62 (2020)
- Marius E. Yamakou, Jürgen Jost: Control of coherence resonance by self-induced stochastic resonance in a multiplex neural network, Physical Review E 100, 022313 (2019)
|| Go to the Math & Research main page