Nonlocal population balance equations and applications
Motivational example: look ahead behavior of car drivers
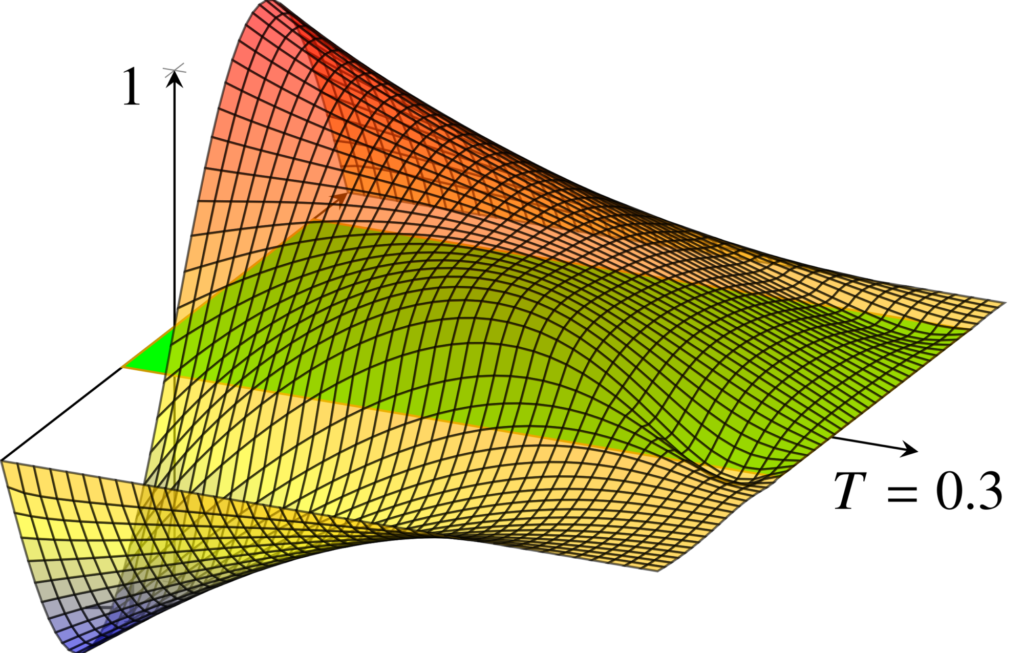
When analyzing traffic situations, one possible way to observe the current state is from bird’s eye view. The velocity of a car driver at time at location depends on the traffic density at time :
High density ⇒ driver slows down or stops
Low density ⇒ driver accelerates
Problematic scenario: The velocity of the driver depends on the traffic density only in the immediate neighborhood (local information). By this, a preceding traffic jam remains unconsidered and the car driver could crash into the congestion.
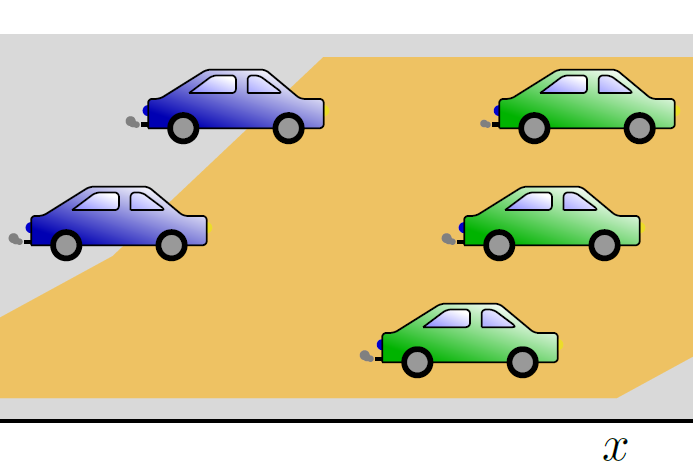
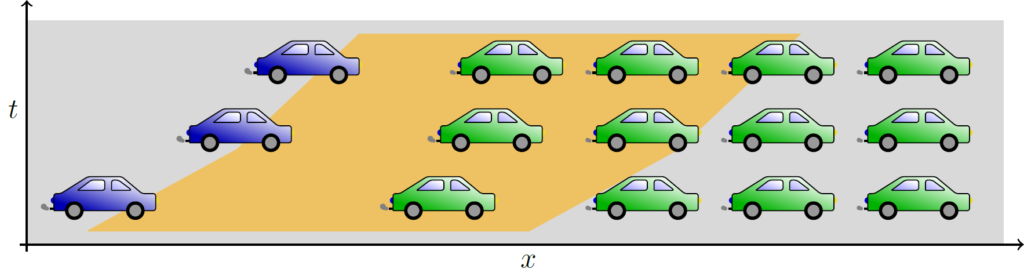
The issue can be avoided when relying on nonlocal information. Here, the velocity also depends on the foregoing traffic situation with a larger distance to oneself. When the car driver is approaching a congestion while the traffic density right in front of him is low, the car driver slows down and a crash can be prevented. This looking ahead behavior is illustrated in Figure 1.
Figure 1. Temporal development of traffic situation. Nonlocal impact: The blue car adjusts its velocity by its driver looking ahead with a range colored in gold and slows down when approaching the green cars (adapted from [2])
What are nonlocal population balance equations (PBEs)?
These are nonlinear conservation laws with velocity function depending on the integral of the solution.
The following representation of the nonlocal PBE is based on [1]
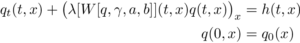 with
with
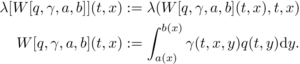
The upper terms are described as follows

Existence, uniqueness and regularity of weak solutions for the mentioned Cauchy-problem, for a related multi-dimensional initial value problem and also for a related initial boundary value problem under weak regularity of data could be shown.
One remarkable aspect: weak solutions are per se unique such that, in comparison to local conservation laws, no additional conditions, such as the well-known Kruzkov Entropy condition are required.
What are real-world applications of nonlocal PBEs?
These equations find a broad application in different sectors. For instance
-
Sedimentation processes
-
Opinion formation
-
Supply chains
-
Traffic flow: look ahead behavior of vehicle drivers
-
Chemical engineering: dependency of ripening of particles with respect to the total surface or the total mass of the particles in the reaction medium
References
[1] Keimer, A., & Pflug, L. (2017). Existence, uniqueness and regularity results on nonlocal balance laws. Journal of Differential Equations, 263(7), 4023–4069
[2] Keimer, A., Pflug, L., & Spinola, M. (2018). Nonlocal scalar conservation laws on bounded domains and applications in traffic flow. SIAM Journal on Mathematical Analysis, 50(6), 6271-6306
|| Go to the Math & Research main page