Partially dissipative hyperbolic systems without Fourier analysis
1 Models
We study the large-time behavior of the one-dimensional partially dissipative hyperbolic system
\begin{aligned} &\partial_t U + A(U)\partial_xU =-BU, & (x,t)\in \mathbb{R}\times \mathbb{R}_{+}, \end{aligned} (1.1)
where U=U(t,x)\in \mathbb{R}^{n} (n\geq2) is the vector-valued unknown, A:\mathbb{R}^n\rightarrow\mathbb{R}^{n\times n} is a smooth matrix-valued symmetric function and B is a positive semidefinite symmetric n\times n matrix. System (1.1) models non-equilibrium processes in physics for media with hyperbolic responses and also arises in the numerical simulation of conservation laws by relaxation schemes.
We assume that (1.1) has a partially dissipative structure: the matrix B takes the form
\begin{aligned} B=\begin{pmatrix} 0 & 0 \\ 0 & D \end{pmatrix} \end{aligned} (1.2)
with D a positive definite symmetric n_2\times n_2 matrix (1\leq n_{2} \lt n). Under these conditions, D satisfies the strong dissipativity condition: there exists a constant \kappa>0 such that, for all X\in\mathbb{R}^{n_{2}},
\begin{aligned} \langle DX,X\rangle\geq \kappa |X|^2, \end{aligned} (1.3)
where \langle\:,\rangle denotes the inner product in \mathbb{R}^n.
A classical system fitting the description (1.1)-(1.2) is the compressible Euler equations with damping:
\left\{ \begin{aligned} &\partial_{t}\rho+\partial_x (\rho u)=0,\\ &\partial_{t} (\rho u)+\partial_x (\rho u^2)+\partial_x P(\rho)=-\lambda \rho u, \end{aligned}\right. (1.4)
where \rho=\rho(x,t)\geq 0 denotes the fluid density, u=u(x,t)\in\mathbb{R} stands for the fluid velocity, P(\rho) is the pressure function, and the friction coefficient \lambda>0 is assumed to be constant. For a \gamma-law pressure with the adiabatic coefficient \gamma>1, a standard symmetrization procedure allows to rewrite system (1.4) into the symmetric form (1.1):
\left\{ \begin{aligned} &\partial_{t}c+u\partial_x c+\frac{\gamma-1}{2}c\partial_x u=0,\\ &\partial_{t}u+u\partial_x u+\frac{\gamma-1}{2}c\partial_x c=-\lambda u, \end{aligned}\right. (1.5)
where c:=2/(\gamma-1)\sqrt{\partial P(\rho)/\partial\rho} is a multiple of the speed of sound. System (1.4) describes compressible gas flows passing through porous media.
We are also interested in partial nonlinear dissipation phenomena of the nonlinearly damped p-system:
\left\{ \begin{aligned} & \partial_t \rho+\partial_x u=0,\\ &\partial_t u+\partial_x \rho +|u|^{r-1}u=0,\\ &(\rho,u)(x,0)=(\rho_{0},u_{0})(x), \end{aligned}\right. (1.6)
with r>1. For small velocities |u|\ll1, system (1.6) is often used to model gas networks.
Fourier analysis is a very important tool in the study of linear and nonlinear PDEs, particularly for the partially dissipative hyperbolic systems (1.1). Their inherent frequency dependence has led most studies of their large-time asymptotics to rely on Fourier analysis, refer to many important works [1-4, 9, 12-14] and references therein. However, Fourier analysis may have a few limitations: it is not easily applied to equations set on bounded or exterior domains, it can make it harder to extract beneficial properties from nonlinear terms, e.g., for (1.6), and it is not well suited to analyse numerical schemes on non-uniform meshes.
Our goal is to develop the “physical space version” of the hyperbolic hypocoercivity approach introduced by Beauchard and Zuazua in [1] so as to derive and pave the way for new asymptotic results which can not be obtained via Fourier analysis.
2 Shizuta-Kawashima condition and Kalman rank condition
The partially dissipative nature (1.2) does not play a role when studying its local well-posedness but is crucial to justifying large-time results. For B=0, (1.1) reduces to a system of hyperbolic conservation laws, and it is well-known that for smooth initial data there exist local-in-time solutions that may develop singularities (shock waves) in finite time, see e.g. [6]. On the other hand, when \textrm{rank}(B)=n, Li [10] proved the existence of global-in-time solutions that are exponentially damped. In our partially dissipative setting (1.2), i.e. \textrm{rank}(B)\lt n, the dissipation induced by BU lacks coercivity, as it affects only some components of the solution.
To complete the dissipative structures for large time, Shizuta and Kawashima in [12] introduced a stability condition (called Shizuta-Kawashima condition):
\begin{aligned} \{\text{eigenvectors of } A \} \cap \mathrm{Ker}(B) = \{0\}. \end{aligned} (SK)
Condition (SK) reveals that interaction effects between the hyperbolic and dissipative parts of the system may generate dissipation in directions that are not affected by B.
More recently, Beauchard and Zuazua [1] have framed this phenomenon in the spirit of Villani’s hypocoercivity theory [15]. Below, we present some key points of their approach.
Linearizing system (1.1)-(1.2) around a constant equilibrium \bar{U}\in \text{Ker}(B) and denoting A:=A(\bar{U}), we obtain the linear system
\begin{aligned} &\partial_t U + A\partial_xU =-BU. \end{aligned} (2.1)
To further highlight the partially dissipative structure of (2.1)-(1.2), we write U=(U_1,U_2) where U_1\in \textrm{Ker}(B)=\mathbb{R}^{n_1} and U_2\in \textrm{Im}(B)=\mathbb{R}^{n_2} with n_{1},n_{2} satisfying 1\leq n_{1}, n_{2} \lt n and n_{1}+n_{2}=n. System (2.1) can be rewritten as follows
\begin{aligned} \left\{ \begin{matrix} \displaystyle \hspace{-0.8cm}\partial_tU_1 + A_{1,1}\partial_{x}U_1+ A_{1,2}\partial_{x}U_2=0,\\ \displaystyle \partial_tU_2 + A_{2,1}\partial_xU_1+ A_{2,2}\partial_x U_2=-D U_2, \end{matrix} \right. \quad \text{where } A=\begin{pmatrix} A_{1,1} & A_{1,2} \\ A_{2,1} & A_{2,2} \end{pmatrix} \end{aligned} (2.2)
and with the initial datum (U_1,U_2)(x,0)=(U_{1,0},U_{2,0})(x).
Using the symmetry of A and condition (1.3), one has the energy dissipation law
\begin{aligned} \dfrac{1}{2}\dfrac{d}{dt}\|(U_1,U_2)(t)\|_{L^2}^2+\kappa\|U_2(t)\|_{L^2}^2\leq0. \end{aligned} (2.3)
The law (2.3) demonstrates a lack of coercivity as only dissipation for the component U_2 is observed. To recover dissipation for U_1, in [1], the authors first apply the Fourier transform to (2.1), which yields the parameterized ODE
\begin{aligned} \partial_t\widehat{U}+i\xi A \widehat{U}+B\widehat{U}=0. \end{aligned} (2.4)
Then, a key observation is that, for \xi\ne 0, the exponential stability of the solutions of (2.4) is equivalent to the Kalman rank condition:
\begin{aligned} \text{the matrix }\:\mathcal{K}(A,B):=(B,BA,\ldots,BA^{n-1})^T\quad \text{has full rank } n. \end{aligned} (K)
Such a result, established for instance in [8] in the context of control theory, shows that large-time stability can hold even if the rank of the dissipative matrix is not full.
For hyperbolic systems, results in the same vein can be obtained, but due to the presence of the parameter \xi, specially as \xi\to 0, the uniform exponential stability may not be expected.
In order to get decay estimates with explicit control on the dependence of the frequency parameter \xi, inspired by hypocoercivity arguments, in [1] the following Lyapunov functional was introduced:
\mathcal{L}_{\xi}(t):=|\widehat{U}|^2+\min\{\frac{1}{|\xi|},|\xi|\} {\rm Re} \sum_{k=1}^{n-1} \varepsilon_k \langle BA^{k-1}\widehat{U}, BA^k\widehat{U}\rangle. (2.5)
The following proposition plays a fundamental role when quantifying the decay rates in terms of the rank conditions.
Proposition 2.1([1])
Let A and B be symmetric matrices such that B satisfies (1.2). The following conditions are equivalent.
• System (2.1) is polynomially stable and behaves as the heat equation for large times.
• The pair (A,B) verifies the condition (SK).
• The pair (A,B) verifies the condition (K).
• For every y\in \mathbb{C}^n, there exist constants c,C>0 such that
\begin{aligned} c|y|^2\leq \sum_{k=0}^{n-1} |BA^{k}y|^2 \leq C|y|^2. \end{aligned} (2.6)
For some well-chosen parameters \varepsilon_k in (2.5), differentiating (2.5), differentiating (2.5) with respect to time and using the fact that (2.6) defines a full norm, we obtain
\begin{aligned} |\widehat{U}(\xi,t)|^2\lesssim |\widehat{U_{0}}(\xi)|^2e^{-\gamma_{*}\min\{1,|\xi|^2\}t}, \end{aligned} (2.7)
for some constant \gamma_{*}>0 and all frequencies \xi, which leads to the exponential decay for high frequencies and heat-like polynomial decay for low frequencies.
We recall the classical result about time asymptotics for (1.1) under the L^1 assumption on the initial data based on the use of Condition (SK) or Condition (K) to (2.4) in the frequency space.
Theorem 2.1([1,12])
Let U_0\in L^1\cap L^2, A be a symmetric matrix and B a matrix satisfying (1.2) and (1.3). Then the following assertions are equivalent:
• The pair (A,B) satisfies Condition (SK).
• The pair (A,B) satisfies Condition (K).
• The solution U of (1.1) satisfies
\Vert U^\ell(t) \Vert_{L^{\infty}} \le C t^{-\frac{1}{2}} \Vert U_0 \Vert_{L^1}, \quad\Vert U^h(t) \Vert_{L^2} \le C e^{-\gamma_{*} t} \Vert U_0 \Vert_{L^2}, \quad \|U(t)\|_{L^2} \leq C t^{-\frac{1}{4}} \Vert U_0 \Vert_{L^2} (2.8)
with U^{\ell}(\xi,t):=\widehat{U}(\xi,t)\mathbf{1}_{\{|\xi| \lt 1\}} and U^h(\xi,t):=\widehat{U}(\xi,t)\mathbf{1}_{\{|\xi|>1\}}, where \xi\in\mathbb{R} is the frequency parameter.
In addition, if U_0\in H^1, then we have
\begin{aligned} \|U(t)\|_{\dot{H}^1} \leq C t^{-\frac{3}{4}} \Vert U_0 \Vert_{H^1}. \end{aligned} (2.9)
3 Main results
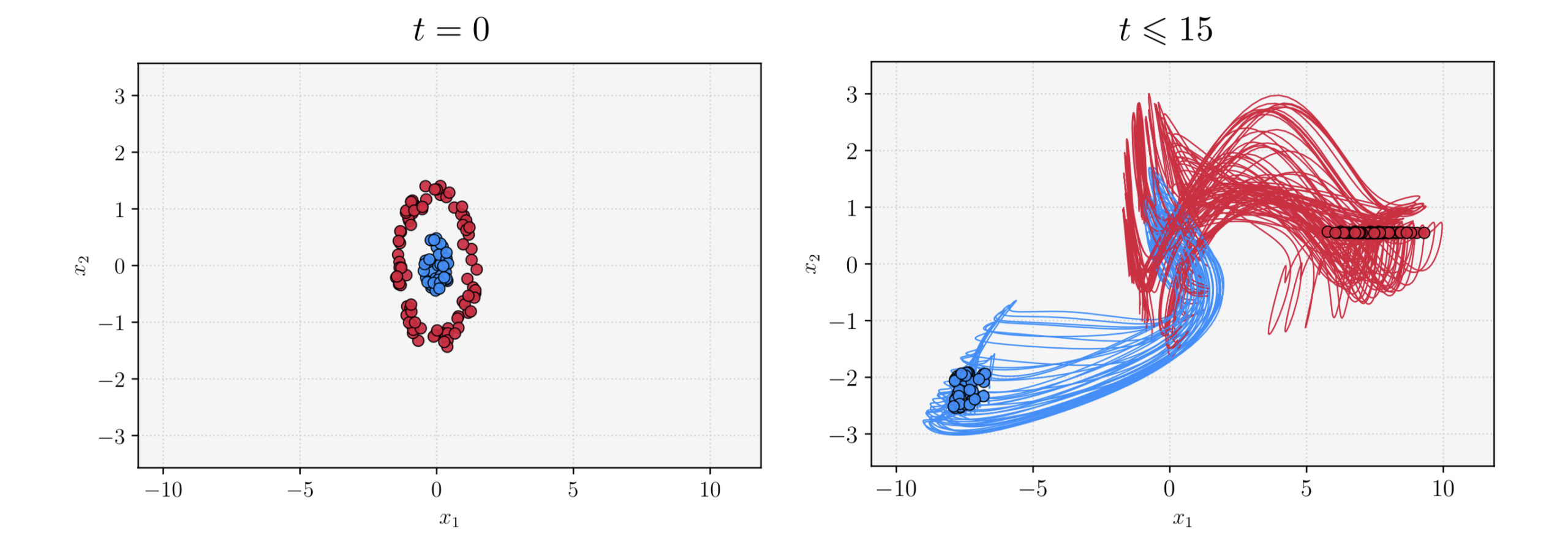
In the recent work [5], we develop the physical space version of the frequency dependent hypocoercivity calculus presented above. First, we recover the optimal time-decay rate for the linearization of one-dimensional partially dissipative linear systems without using Fourier analysis and establish enhanced rates for initial data belonging to weighted Sobolev spaces. Then, we apply our new analysis to study the large time asymptotics of two concrete nonlinear systems: the compressible Euler equations with linear damping and the p-system with nonlinear damping.
3.1 Natural time-decay rates without Fourier analysis
In our first result, we retrieve the natural large-time asymptotics of linear partially dissipative hyperbolic systems (2.1) without using Fourier analysis or L^1-type assumptions on the initial data.
Theorem 3.1
Let U_{0}\in H^1, A and B be symmetric n\times n matrices with B as in (1.2), satisfying Condition (K). Then, the solution U of (2.1) with the initial datum U_{0} satisfies
\| U_2(t)\|_{L^2}+\|\partial_x U(t)\|_{L^2} \leq C(1+t)^{-\frac{1}{2}}\|U_0\|_{H^1}. (3.1)
According to Proposition 2.1, the rate obtained for U in estimate (3.1) is sharp in our Hilbertian functional framework. It actually corresponds to that of the heat equation. Unlike Fourier-based approaches, our method is not well suited to exploiting the L^1 control of the initial data. However, it is adaptable to weighted spaces, as we will see in the next results.
Strategy of proof of Theorem 3.1. The core of the proof is the construction of an augmented energy functional in the spirit of (2.5) but entirely defined in the physical space. Inspired by the works of Hérau [7] and Porretta and Zuazua [11], concerning the asymptotic decay of kinetic equations, we consider the time-weighted functional
\begin{aligned} \mathcal{L}(t)= \|U(t)\|_{H^1}^2+\eta_{0} t\|\partial_x U(t)\|_{L^2}^2+\sum_{k=1}^{n-1} \varepsilon_k \langle BA^{k-1}U,BA^k\partial_xU\rangle_{L^2}. \end{aligned} (3.2)
Setting the constants \eta_{0} and \varepsilon_{k}, k=1,2,...,n-1, suitably small and using the Kalman rank condition, we obtain
\begin{aligned} \frac{d}{dt}\mathcal{L}(t)+\|\partial_x U(t)\|_{L^2}^2+\|U_{2}(t)\|_{L^2}^2\leq 0, \end{aligned} (3.3)
from which we infer
\begin{aligned}\|\partial_xU(t)\|_{L^2}\lesssim (1+t)^{-\frac12}\|U_0\|_{H^1}. \end{aligned} (3.4)
Then, combining (3.4) with the fact that U_2 verifies a damped equation with linear source terms A_{2,1}\partial_{x}U_1 and A_{2,2}\partial_{x}U_2, Grönwall’s inequality yields the extra decay for U_2 stated in (3.1). Refer to [5] for the details.
3.2 Enhanced decay rates in weighted Sobolev spaces
As depicted in Proposition 2.1, the solutions of (2.1) behave similarly to the solutions of the heat equation as the time evolves. More precisely, they decay as the solutions of the parabolic system
\left\{ \begin{aligned} &\partial_{t}N-A_{1,2}D^{-1}A_{2,1} \partial^2_{x}N=0,\\ &N(x,0)=U_{1,0}(x), \end{aligned} \right. (3.5)
where the operator -A_{1,2}D^{-1}A_{2,1}\partial_x^2 is strongly elliptic when the Kalman rank condition (K) holds.
Our next theorem justifies the validity of the large-time parabolic profile (3.5) of the system (2.1) without Fourier analysis and provides new enhanced time-decay rates when the initial datum belongs to weighted Sobolev spaces.
Theorem 3.2
Let the hypotheses of Theorem 3.1 be satisfied and let Ube the solution of (2.1) with the initial datum U_0. In addition, suppose also that [kate]|x| U_{2,0} \in L^2[/katex] and A_{1,1}=0. Then, for all t>0 and 0 \lt \varepsilon \ll1/2,
\begin{aligned} &\|(U_1-N)(t)\|_{L^2}\leq C(1+t)^{-\frac{1}{2}+\varepsilon} (\|U_0\|_{H^1}+\| |x| U_{2,0}\|_{L^2}), \end{aligned} (3.6)
where N is the solution of (3.5) associated to the initial datum U_{1,0} and C>0 is a constant independent of time and U_{0}.
Furthermore, let 0 \lt \mu\leq 1. If we further assume
\begin{aligned} X_0:=\|U_{0}\|_{H^1}+\||x|^{\mu}U_{1,0}\|_{L^2}+\| |x| U_{2,0}\|_{L^2} \lt \infty, \end{aligned} (3.7)
then, for all t>0,
\left\{ \begin{aligned} &\|U(t)\|_{L^2}\leq C (1+t)^{-\frac{\mu}{2}}X_0,\\ &\|U_2(t)\|_{L^2}+\|\partial_x U(t)\|_{L^2}\leq C(1+t)^{-\frac{\mu}{2}-\frac{1}{2}}X_0. \end{aligned} \right. (3.8)
The time-decay rates obtained for U in Theorem (3.2) are optimal as they coincide with the rates of the heat equation.
When \frac{1}{2}\lt\mu\leq1, the assumption X_0\lt\infty is a stronger condition than the L^1 assumption usually used in Fourier-based approaches, but it allows for faster decay rates. For \mu=1/2, which is an inaccessible limit case for our method, the rate in (3.8)_1 would correspond to the one recovered with Fourier analysis and for initial data belonging to L^1 (cf. Theorem 2.1).
3.3 Application to the compressible Euler equations with damping
In our next result, we justify a nonlinear analogue of Theorem 3.1 for the compressible Euler system with linear damping (1.4), when the initial data are close to a constant equilibrium in H^2.
Theorem 3.3
Consider the equilibrium state (\bar{\rho},0), with \bar{\rho}>0 a given constant, and suppose P'(\rho)>0. Then, there exists a constant \delta_0>0 such that if the initial datum (\rho_{0},u_{0}) satisfies
\begin{aligned} &\|(\rho_{0}-\bar{\rho},u_{0})\|_{H^{2}}\leq \delta_{0}, \end{aligned} (3.9)
System (1.4) admits a unique global-in-time solution (\rho,u) satisfying
\begin{aligned} & \|u(t)\|_{L^2}+\|\partial_x (\rho-\bar{\rho},u)(t)\|_{L^2}\leq C(1+t)^{-\frac{1}{2}}\|(\rho_{0}-\bar{\rho},u_{0})\|_{H^{2}}. \end{aligned} (3.10)
The next result corresponds to nonlinear versions of Theorem (3.2) for System (1.4). Due to the nonlinear term arising from the pressure, the decay rate for the error unknown in (3.12) is slower than the linear case in (3.6).
Theorem 3.4
Assume that the hypotheses of Theorem 3.3 are satisfied. Let \mu> 1/2. If, in addition to (3.12), we assume |x| u_{0}\in L^2 , then the solution (\rho,u) for System (1.4) satisfies
\left\{ \begin{aligned} &\|(\rho-\bar{\rho})(t)\|_{L^2}\leq C (1+t)^{-\frac{\mu}{2}},\\ & \|u(t)\|_{L^2}+\|\partial_x (\rho-\bar{\rho},u)(t)\|_{L^2}\leq C (1+t)^{-\frac{\mu}{2}-\frac{1}{2}}. \end{aligned}\right. (3.11)
If, in addition to (3.9), we assume |x| u_{0}\in L^2 . Then, for all t>0 and 0\lt\varepsilon\ll1/4, there exists a constant independent of T such that
\begin{aligned} &\|(\rho-\rho_*)(t)\|_{L^2}\leq C (1+t)^{-\frac{1}{4}+\varepsilon}, \end{aligned} (3.12)
where \rho_* solves the parabolic equation
\left\{ \begin{aligned} &\partial_{t}\rho_*-\frac{P'(\bar{\rho})}{\lambda}\partial_x^2 \rho_*=0,\\ &\rho_*(0,x)=\rho_0(x). \end{aligned} \right. (3.13)
Furthermore, for any 0\lt\mu\leq 1, we further assume |x|^{\mu}(\rho_{0}-\bar{\rho})\in L^2, then, for all t>0,
\left\{ \begin{aligned} &\|(\rho-\bar{\rho})(t)\|_{L^2}\leq C (1+t)^{-\frac{\mu}{2}},\\ & \|u(t)\|_{L^2}+\|\partial_x (\rho-\bar{\rho},u)(t)\|_{L^2}\leq C (1+t)^{-\frac{\mu}{2}-\frac{1}{2}}. \end{aligned} \right. (3.14)
3.4 Application to the nonlinearly damped p-system
Our final result concerns nonlinear dissipative phenomena. With the aid of the hypocoercive arguments beofore, we justify the logarithmic stability of System (1.6) when the initial data belong to logarithmically weighted Sobolev spaces.
Theorem 3.5
Let 1 \lt r \lt 3 and suppose that (\rho_{0},u_{0})\in H^1 . Then, for all t>0, System (1.6) admits a unique global-in-time solution (\rho,u)\in C(\mathbb{R}_{+};H^1 ). Furthermore, let q>0 and suppose that
\begin{aligned} \rho_0 \in L^1 \quad \textrm{and} \quad \log^{q}{(1+ |x|)} (\rho_{0},u_{0})\in L^2. \end{aligned} (3.15)
Then, it holds that
\begin{aligned} &\| (\rho,u)(t)\|_{L^2}\leq \frac{C}{\log^{q}(1+t)}. \end{aligned} (3.16)
Conclusions
In the work [5], we lay the foundations for hyperbolic hypercoercivity without resorting to Fourier analysis. This enables us to extend the analysis of partially dissipative hyperbolic systems to previously unexplored contexts.
Furthermore, our approach provides a guideline for future investigations on partially dissipative systems in many contexts which can not be analyzed via Fourier analysis, such as initial boundary value problems on bounded or exterior domains, more general nonlinearly damped systems, space-dependent hyperbolic matrices, and numerical approximation schemes on non-uniform meshes.

Post made during my visit at FAU DCN-AvH, in the photo (left to right): Prof. Enrique Zuazua, Ling-Yun Shou, Dr. Timothée Crin-Barat
References
[1] K. Beauchard, E. Zuazua, Large time asymptotics for partially dissipative hyperbolic systems, Arch. Ration. Mech. Anal., 199:177-227, 2011.[2] S. Bianchini, B. Hanouzet, R. Natalini, Asymptotic behavior of smooth solutions for partially dissipative hyperbolic systems with a convex entropy, Comm. Pure Appl. Math., 60:1559-1622, 2007.
[3] T. Crin-Barat, R. Danchin, Partially dissipative one-dimensional hyperbolic systems in the critical regularity setting, and applications, Pure and Applied Analysis, 4(1):85-125, 2022.
[4] T. Crin-Barat, R. Danchin, Partially dissipative
hyperbolic systems in the critical regularity setting : {T}he multi-dimensional case, J. Math. Pures Appl. (9), 165:1-41, 2022.
[5] T. Crin-Barat, L.-Y. Shou, E. Zuazua, Large time asymptotics for partially dissipative hyperbolic systems without Fourier analysis: application to the nonlinearly damped p-system, Arxiv: 2308:08230.
[6] C. M. Dafermos, Hyperbolic Conservation Laws in Continuum Physics, 3rd edition, Grundlehren Math. Wiss., Vol. 325, Springer, Heidelberg, Dordrecht, London and New York, 2010.
[7] F. Hérau, Short and long time behavior of the {F}okker-{P}lanck equation in a confining potential and application, J. Func. Anal., 244:95-118, 2007.
[8] R. E. Kalman, P. L. Falb, M. A. Arbib, Topics in Mathematical Control Theory, McGraw-Hill Book Co, New York-Toronto, Ont.-London, 1969, 513-529.
[9] S. Kawashima, Systems of a hyperbolic-parabolic composite type, with applications to the equations of magnetohydrodynamics, Doctoral Thesis, 1983.
[10] T.-T. Li, Global classical solutions for quasilinear hyperbolic systems, Masson, Paris; John Wiley \& Sons, Ltd., Chichester, 1994.
[11] A. Porretta, E. Zuazua, The optimal decay estimates on the framework of {B}esov spaces for generally dissipative systems, Math. Comp., 86(303):97-119, 2017.
[12] S. Shizuta, S. Kawashima, Systems of equations of hyperbolic-parabolic type with applications to the discrete {B}oltzmann equation, Hokkaido Math. J., 14:249-275, 1985.
[13] J. Xu, S. Kawashima, The optimal decay estimates on the framework of {B}esov spaces for generally dissipative systems, Arch. Ration. Mech. Anal., 218:275-315, 2015.
[14] J. Xu, S. Kawashima, Frequency-localization Duhamel principle and its application to the optimal decay of dissipative systems in low dimensions, J. Differential Equations, 261:2670-2701, 2016.
[15] C. Villani, Hypocoercivity, Mem. Am. Math. Soc., 261, 2010.
|| Go to the Math & Research main page