Analysis and Control of Nonlinear Hyperbolic Systems with Degeneration on Networks
DFG WA5144/1-1: Modellierung, Analysis und Steuerung degenerierter nichtlinearer hyperbolischer Systeme auf Netzwerken
- Project/grant No.: 504042427
- Supported by DFG – Deutsche Forschungsgemeinschaft Individual Research Grant
- Duration: 2022 – 2024
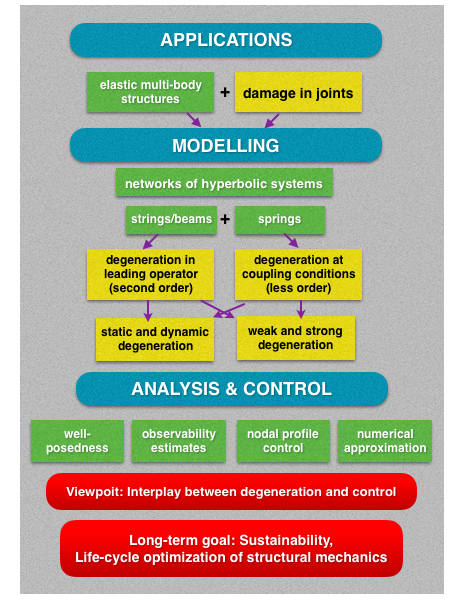
Control for degenerate partial differential equations (PDEs) is needed many applications, in particular, for the cloaking problem (building of devices that lead to lack of observability), the evolution of damage in materials, optimization problems for elastic bodies arising in contact mechanics, coupled systems, composite materials. Moreover, the sustainable control of mechanical structures, which suffer damage and possibly failure due to their dynamics, especially in coupling points, has been viewed as a major issue within the control design on multi-body systems, such as flexible elastic multi-structures interconnected of strings, bars, masses and springs, flexible robotic arms and networks made of pipes. Such a variety of applications has given birth to challenging mathematical problems for degenerate PDEs on networks, with various facets and focal points yet to be explored aspects of the system to be considered.
This project proposal aims at developing an innovative and systematic two-year research agenda, focusing on control problems for elastic bodies arising in particular in structural mechanics, e.g. flexible multi-link structures, pipe-systems, string-mass-spring-systems or highly flexible robots, where degeneration (damage and failure) takes place at the boundaries or in multiple joints. The long-time goal is to develop control strategies that guarantee optimal performance while also respect the life-cycle of the structures.
People involved
Scope/Goal
The scientific goal of the project is to understand the influence of damage effects on the dynamical behavior and controllability properties of networked infinite-dimensional equations and to develop control theory for degenerate hyperbolic systems that can be applied to the nonlinear problems on networks arising in real world applications. To this end, we pursue three objectives: 1) to develop new models for networks of structural elements with damage and failure in joints, 2) to provide rigorous mathematical analyses of these models, and 3) to study the controllability properties of these models such as nodal controllability (also called side-wise controllability), observability, and synchronization.
The control of nonlinear hyperbolic systems with degeneration on networks is a comparatively new and significant topic. The project is founded on the previous research of the applicant on degeneration in partial differential equations and the control of networked hyperbolic systems, especially on strings, beams, and shallow water equations. This experience is complemented by the expertise of several world-leading experts in research institutes in Germany and abroad.
The project focusses on two specific configurations of the damage. In the first one, the damage takes place at one or more given joints. The damage leads to a degeneracy in the leading coefficient which results in a loss of uniform ellipticity and novel transmission conditions. This raises theoretical and practical challenges for the analysis and the control of these systems. The second configuration is one in which the damage occurs in the coupling conditions, e.g. in a degenerating (visco-)elastic spring that couples strings or beams. In each configuration, we consider two types of damage: static degeneration and dynamic degeneration, which are both poorly understood. For the latter type
of damage, the evolution of a damage source function depends on the mechanical compression or tension.
For each of these four types of damage models, the analysis of the underlying dynamics, the mathematical controllability properties of the network (i.e. exact- nodal profile-controllability or synchronization) and the development of numerical schemes for their approximation come hand in hand. This combination is necessary to tackle the challenges posed by degeneration and nonlinearity in networks of PDEs. This project thus forms a valuable and essential step towards the development of model-driven and data-driven control theory for large-scale networks with degeneration that occur in many applications.
See more about this project at DFG
|| Go to the Projects main page










