Clustering in pure-attention hardmax transformers and its role in sentiment analysis

This post provides an overview of the results in the paper Clustering in Pure-Attention Hardmax Transformers and its Role in Sentiment Analysis by Albert Alcalde, Giovanni Fantuzzi, and Enrique Zuazua [1]. Codes used to reproduce the simulations can be found at the repository:
https://github.com/DCN-FAU-AvH/clustering-hardmax-transformers

GitHub Repository

Resources available at our FAU DCN-AvH GitHub, o directly at: https://github.com/DCN-FAU-AvH/clustering-hardmax-transformers.

The transformer [9] is a fundamental model in contemporary machine learning that consistently outperforms traditional deep learning paradigms, such as recurrent neural networks [6], in tasks related to language modeling [2], computer vision [3], and audio processing [8]. The power of transformers is often attributed to the so-called self-attention sublayers, which, heuristically, identify relations between components of the transformer’s input data to facilitate prediction tasks. A rigorous explanation for the role of the self-attention sublayers, however, remains to be given. In our work, we take a step in this direction and provide precise mathematical results that explain the role of self-attention for a simplified but still expressive class of transformers, which we call pure-attention hardmax transformers.

The model

Pure-attention hardmax transformers are parameterized by a symmetric positive definite matrix $A \in \mathbb{R}^{d\times d}$ and a scalar parameter $\alpha > 0$ . They act on a collection of points $z_{1}{},\ldots,z_{n}{} \in \R^d$ , called tokens in the machine learning literature, that we arrange as the rows of a matrix $Z \in \mathbb{R}^{n\times d}$ . In applications, tokens encode components of the transformer input, such as words in a language model or snippets of an image in computer vision. Given initial token values $z_{1}^{0},\ldots,z_{n}^{0}$ , the value $z_{i}^{k+1}$ of token $z_{i}^{k}$ returned by the $k^{th}$ layer of our transformer model is

$z_{i}^{k+1}=z_{i}^{k}+\frac{\alpha}{1+\alpha}\,\frac{1}{|{C_{i}}(Z^k)|}\sum_{j\in {C_{i}}(Z^k)}\Big({z_{j}}^{k}-z_{i}^{k}\Big), \qquad (1.1a)$

where $Z^k$ is the token matrix in layer $k$ and

${C_{i}}(Z^k)= \left\{ j\in [n]\,\, : \,\, \big\langle A z_{i}^{k}, z_{j}^{k}\big\rangle = \max_{\ell\in[n]} \big\langle A z_{i}^{k}, z_{\ell}^{k}\big\rangle \right\}. \qquad (1.1b)$

In these equations, $|{C_{i}}(Z^k)|$ is the cardinality of the index set ${C_{i}}(Z^k)$ , angled brackets denote the standard inner product in $\R^d$ , and $[n]=\{1,\ldots,n\}$ . We note that, if we view (1.1) as a discrete-time dynamical system describing the evolution of tokens (see [4,5,7] for more on this dynamical perspective), then the self-attention mechanism has a simple geometric interpretation: token $z_{i}^{k}$ is attracted to the tokens with the largest orthogonal projection in the direction of $A z_{i}^{k}$ (cf. Figure 1), with the parameter $\alpha$ acting as a step-size that regulates the intensity of the attraction.

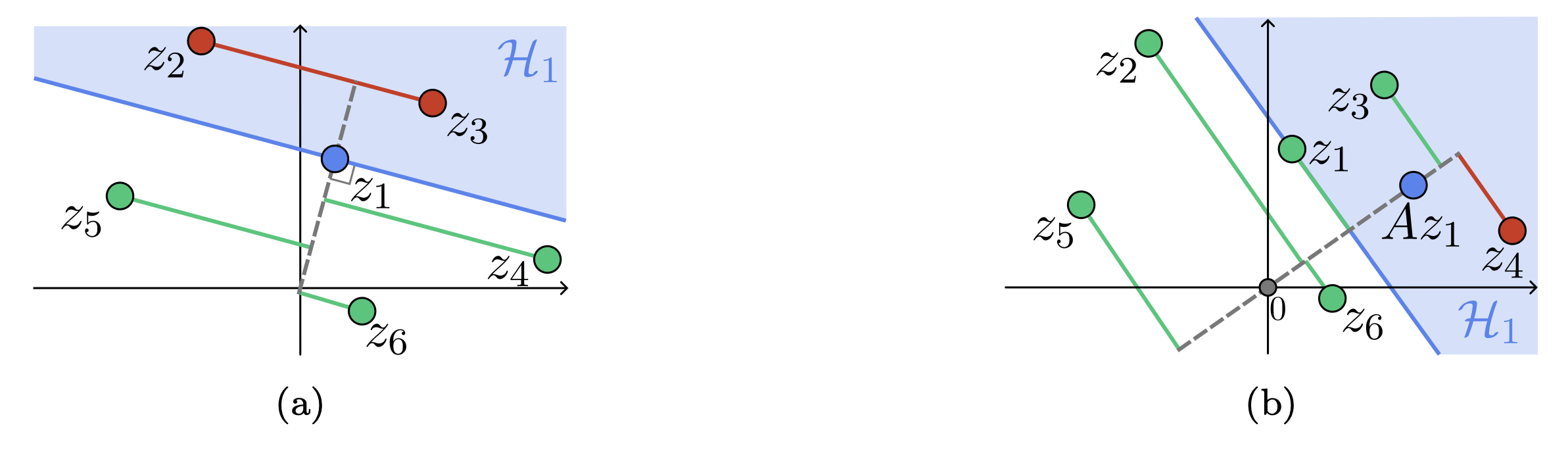
Figure 1. Geometric interpretation of (1.1b) for $i=1$ with (a) $A=I$ and (b) $A = \begin{pmatrix} 2 & 1 \\ 1 & 1 \end{pmatrix}$

Contributions

Motivated by the ever increasing depth of transformers (for instance, GPT-3 includes up to 96 layers [2]), we study the asymptotic behavior of tokens that start from given initial values $z_{1}^{0}, \dots, z_{n}^{0} \in \R^d$ and evolve according to (1.1). We prove that, as $k\to \infty$ , tokens converge to a clustered equilibrium where the cluster points are either special tokens that we call leaders, or particular convex combinations thereof.

Definition 2.1
Token $z_{i}^{k}$ is a leader if there exists a layer $k \in \N$ such that ${C_{i}}(Z^k) = \{ i \}$ .

Theorem 2.1
Assume the initial token values $z_{1}^{0},\ldots,z_{n}^{0} \in \R^d$ are nonzero and distinct. Assume also the matrix $A\in \R^{d\times d}$ in (1.1b) is symmetric and positive definite. Then, the set of leaders $\mathcal{L}$ is not empty, and there exist a convex polytope $\mathcal{K}$ with $| \mathcal{L} |$ vertices and a finite set $\mathcal{S} \subset \partial \mathcal{K}$ such that:
(i) Every token converges to a point in $\mathcal{S}$ .
(ii) Every leader converges to a distinct vertex of $\mathcal{K}$ in finite layers.
(iii) If $s\in \mathcal{S}$ is not a vertex of $\mathcal{K}$ , then it is a projection of the origin onto a face of $\mathcal{K}$ with respect to the norm associated with $A$ .

Having demonstrated that pure-attention hardmax transformers modeled by (1.1) exhibit clustering, we now apply our theoretical insights to practice by building an interpretable transformer model for sentiment analysis. The task is to predict whether a movie review is positive or negative. Our minimal classifier model comprises three explainable components:
• Encoder: Maps words in a review to tokens in $\mathbb{R}^d$ and selects meaningful words as leaders.
• Our Transformer (1.1) Captures context by clustering tokens around the leaders.
• Decoder: Projects token values after the last transformer layer to a positive or negative sentiment prediction.

We train our model on a range of movie reviews and confirm our interpretation with examples (see Figure 2), showing that leaders correspond to meaningful words and that our transformer captures context by clustering most words around the leaders.

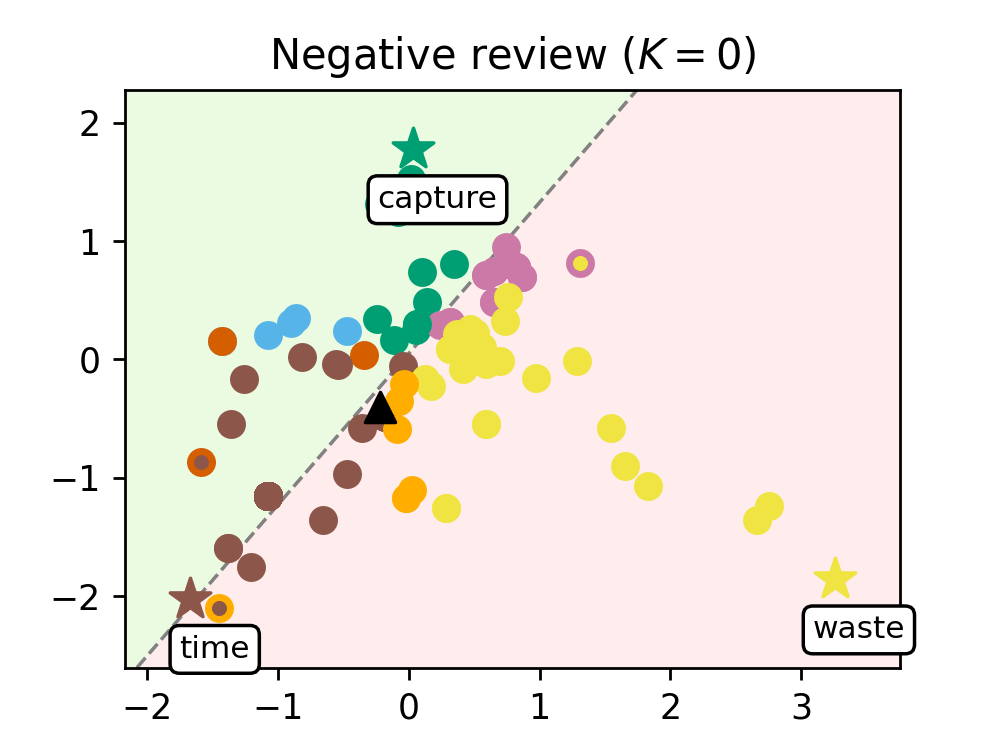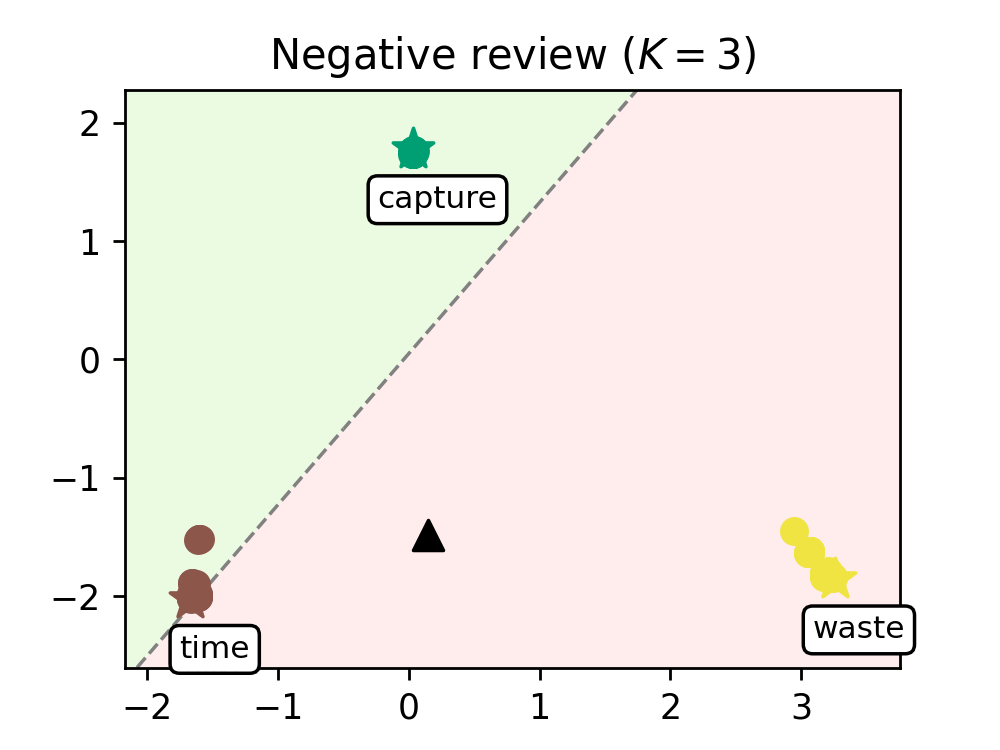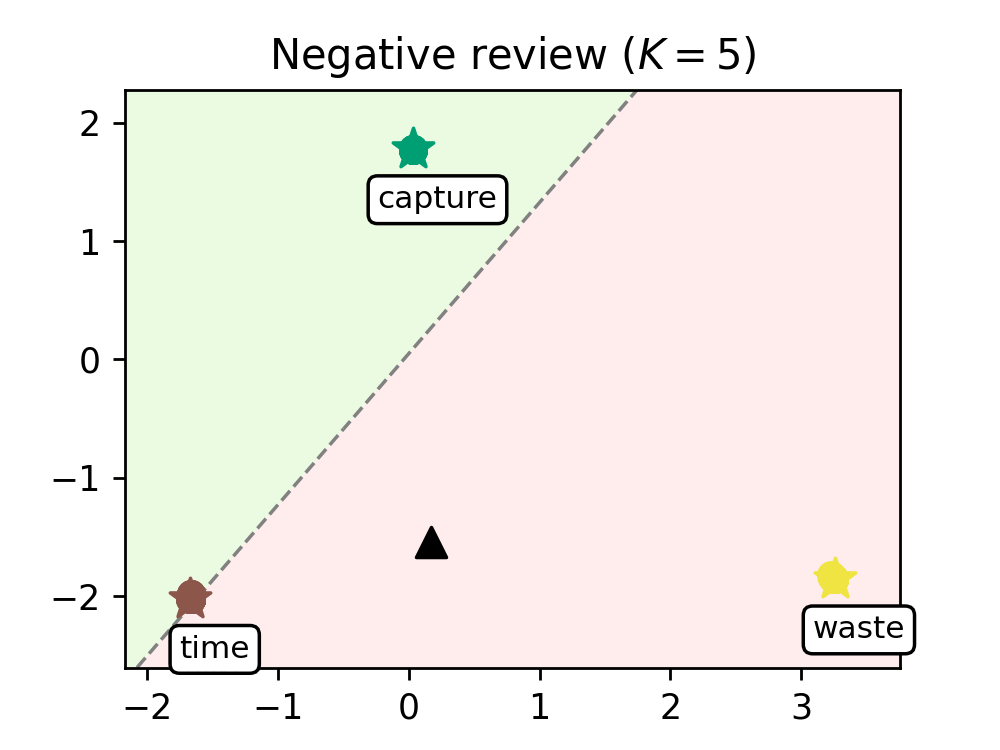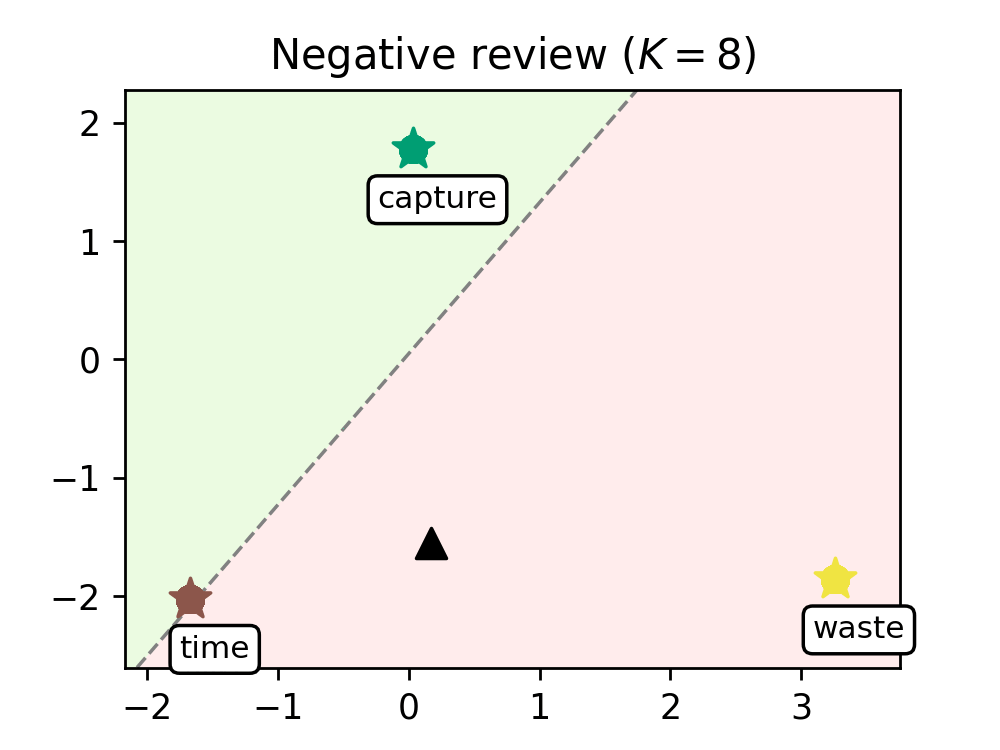
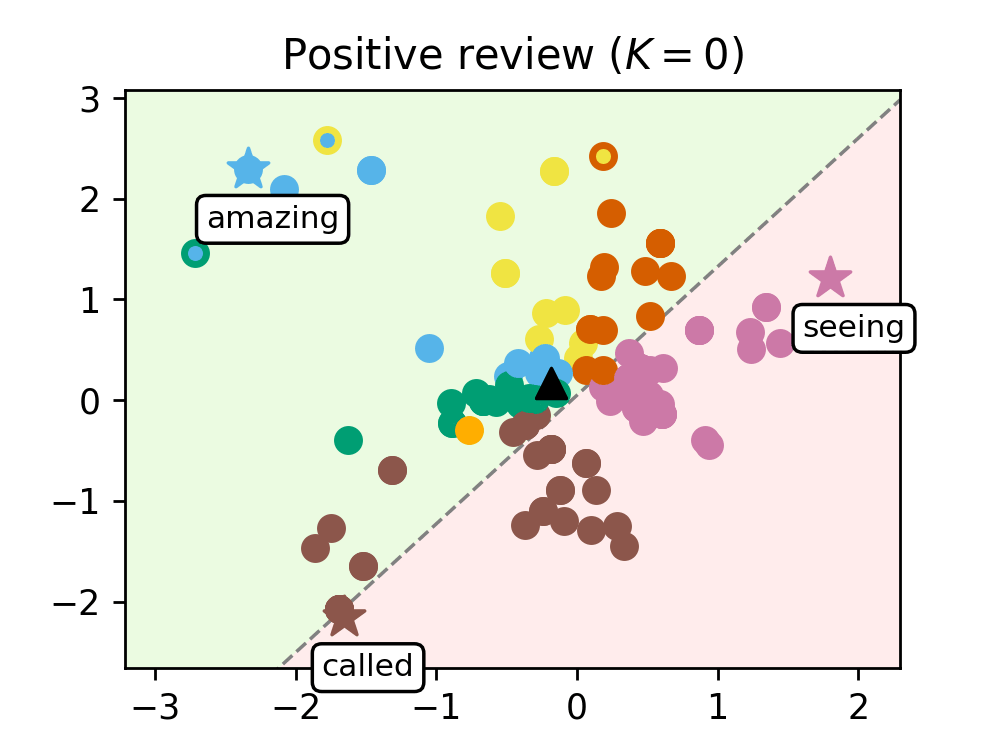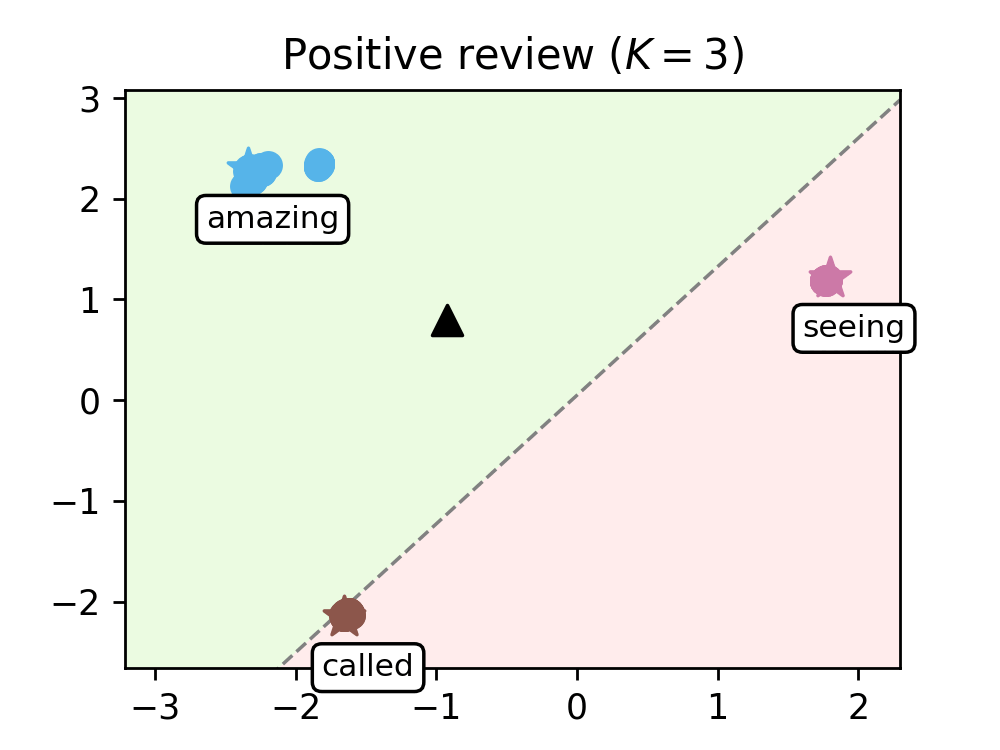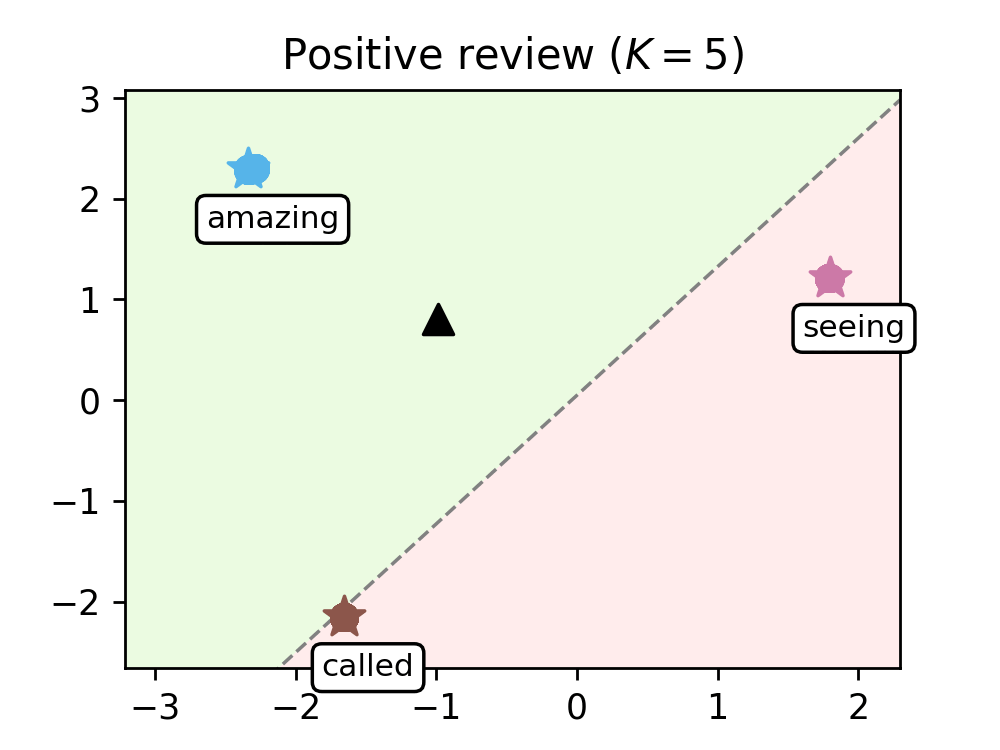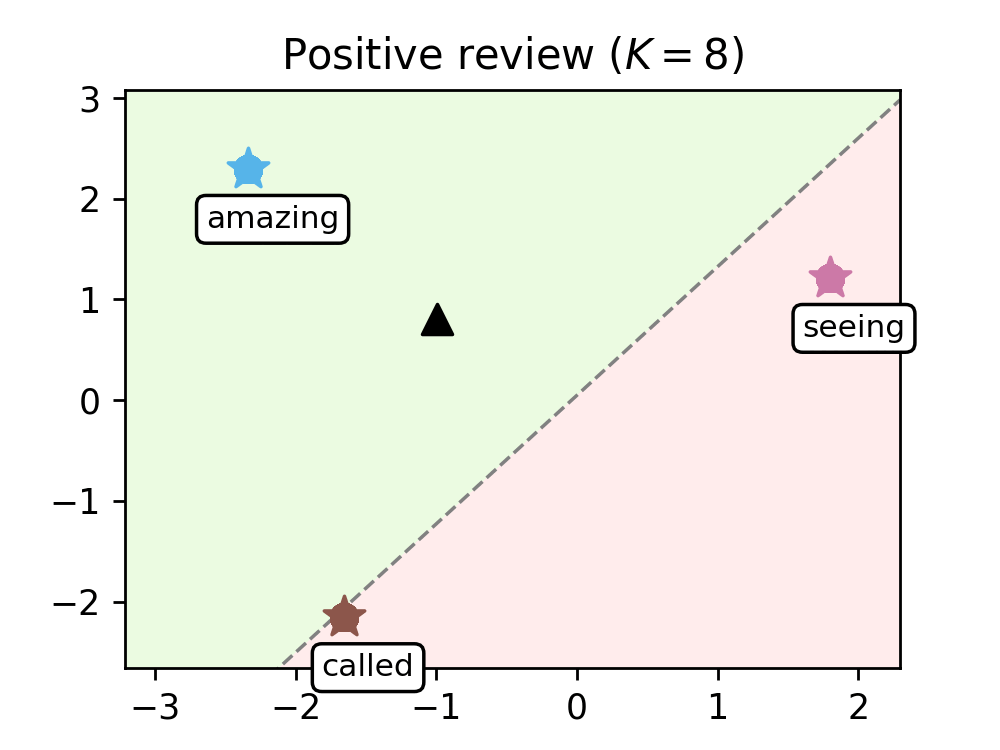
Figure 2. Evolution of the words of a negative review (left) and a positive review (right), as they are processed by the $K=8$ transformer layers. Leaders are represented with stars and tagged with the word they encode, circles are the remaining tokens, and the black triangle is the average token. The dashed line represents the hyperplane separating the half-plane identified with the positive class (shaded in green) from the one identified with the negative class (shaded in red).

Structure of the repository

We provide a brief overview of the repository where the codes and data used in our paper can be found. The two main files are:
• imdb_classifier.ipynb, where we conduct the numerical experiments for the sentiment analysis of IMDb movie reviews. We read and batch the preprocessed data, define the hyperparameters, train the model and plot the tokens of reviews evolving through the layers of the transformer.
• dynamics.ipynb, where we simulate the dynamics of our transformer by trying different initial configurations. Used to generate Figure 2.

Next, we include a brief description of the folders in the repository:
data folder: contains the original reviews from the IMDb dataset (IMDB Dataset.csv), and the preprocessed reviews (imdb_preprocessed.csv), which are generated with preprocess.py.

plots folder: contains the plots generated by the different files of the repository.

saved folder: contains the weights and parameters of the trained models, as well as the history of the training curves (loss and accuracy).

utils folder: contains the definition of the functions needed in the main files:
• graphics.py, includes the functions needed for plotting the results.
• models.py, includes the definition of our transformer-based classifier, the encoder, hardmax dynamics and decoder.
• training.py, includes the functions needed for the training process.

References

[1] A. Alcalde, G. Fantuzzi, and E. Zuazua. Clustering in pure-attention hardmax transformers and its role in sentiment analysis. In preparation (2024).
[2] T. Brown et al. Language models are few-shot learners. In Advances in Neural Information Processing Systems, volume 33, pages 1877–1901, 2020.
[3] A. Dosovitskiy et al. An image is worth 16×16 words: Transformers for image recognition at scale. In International Conference on Learning Representations, 2021.
[4] B. Geshkovski, C. Letrouit, Y. Polyanskiy, and P. Rigollet. The emergence of clusters in self-attention dynamics. arXiv:2305.05465 [cs.LG], 2023.
[5] B. Geshkovski, C. Letrouit, Y. Polyanskiy, and P. Rigollet. A mathematical perspective on Transformers. arXiv:2312.10794 [cs.LG], 2023.
[6] S. Hochreiter and J. Schmidhuber. Long Short-Term Memory. Neural Computation, 9(8): 1735–1780, 11 1997. ISSN 0899-7667.
[7] Y. Lu et al. Understanding and improving transformer from a multi-particle dynamic system point of view. In ICLR 2020 Workshop on Integration of Deep Neural Models and Differential Equations, 2019.
[8] A. Radford, J. W. Kim, T. Xu, G. Brockman, C. Mcleavey, and I. Sutskever. Robust speech recognition via large-scale weak supervision. In Proceedings of the 40th International Conference on Machine Learning, volume 202, pages 28492–28518, 2023.
[9] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin. Attention is All you Need. In Advances in Neural Information Processing Systems, volume 30, 2017.