Date: October 03, 2022
Author: Prof. Dr. Enrique Zuazua
Affiliation: Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany). Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship
Source: SIAM News, Society for Industrial and Applied Mathematics. Pittsburgh, Pennsylvania (USA)
Two recurring questions pertain to the origin, history, and present state of mathematics. The first relates to math’s incredible ability to describe natural, industrial, and technological processes, while the second concerns the unity and interconnectedness of all mathematical disciplines. Here I describe some of the gateways that link two particular mathematical branches: control theory and machine learning (ML). These areas, both of which have very high technological impacts, comprise neighboring valleys in the complex landscape of the mathematics universe.
Control theory certainly lies at the pedestal of ML. Aristotle anticipated control theory when he described the need for automated processes to free human beings from their heaviest tasks [3]. In the 1940s, mathematician and philosopher Norbert Wiener redefined the term “cybernetics”—which was previously coined by André-Marie Ampère—as “the science of communication and control in animals and machines,” which reflected the discipline’s definitive contribution to the industrial revolution. (…)
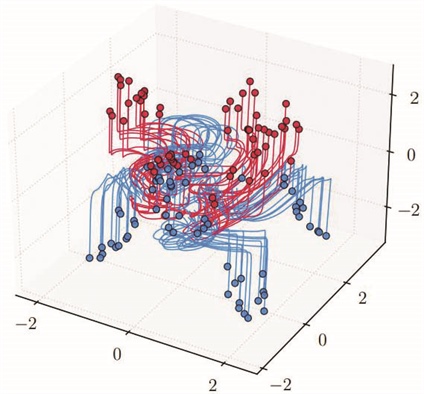
Figure 1. Simultaneous control of trajectories of a neural ordinary differential equation (NODE) for classification according to two different labels (blue/red), exhibiting the turnpike nature of trajectories. Figure courtesy of [5].
It took the mathematical control community many years to understand how to apply control methods to the real challenges of SL. Recent works have finally proved that deep residual neural networks (ResNets)—time discretizations of NODEs—enjoy the amazing and unexpected property of simultaneous or ensemble control [8]. We can build controls (i.e., train parameters) in such a way that an arbitrarily large number of trajectories simultaneously arrive almost exactly at their targets: the labels that correspond to the items of the data set to be classified (see Figure 1).
My colleagues and I are not the first researchers to claim the tight connections between control and ML [4, 7]. But now that we have been working on this topic for several years, we realize that there is still much to discover in the vast forest that connects these two areas. Although finding the paths through the dense grove will be intellectually challenging, doing so may add additional detail to the fascinating global map of the mathematical sciences. These paths will likely take a zigzagged course that resembles the strategies for solving a Rubik’s Cube or the trajectories that assure the needs of learning through ResNet control.(…)
|| Check the complete article at SIAM News
Read the SIAM News (October 2022)
This article is based on Enrique Zuazua’s W.T. and Idalia Reid Prize Lecture at the 2022 SIAM Annual Meeting, which took place this July in Pittsburgh, Pa.
References
[1] Cybenko, G. (1989). Approximation by superpositions of a single function. Math. Control Signals Syst., 2, 303-314.
[2] E, W. (2017). A proposal on machine learning via dynamical systems. Commun. Math. Stat., 5, 1-11.
[3] Fernández-Cara, E., & Zuazua, E. (2003). Control theory: History, mathematical achievements and perspectives. Bol. Soc. Esp. Mat. Apl., 26, 79-140.
[4] Fradkov, A.L. (2020). Early history of machine learning. IFAC-PapersOnLine, 53(2), 1385-1390.
[5] Geshkovski, B., & Zuazua, E. (2022). Turnpike in optimal control of PDEs, ResNets, and beyond. Acta Numer., 31, 135-263.
[6] Kalman, R.E. (1960). On the general theory of control systems. IFAC Proc. Vol., 1(1), 491-502.
[7] LeCun, Y. (1988). A theoretical framework for back-propagation. In D. Touretzky, G.E. Hinton, & T. Sejnowski (Eds.), Proceedings of the 1988 connectionist models summer school (pp. 21-28). Pittsburgh, PA: Carnegie Mellon University.
[8] Ruiz-Balet, D., & Zuazua, E. (2021). Neural ODE control for classification, approximation and transport. Preprint, arXiv:2104.05278.
[9] Sontag, E., & Sussmann, H. (1997). Complete controllability of continuous-time recurrent neural networks. Syst. Control Lett., 30(4), 177-183.
|| Check the complete article at SIAM News





