Limits of the stabilization of a networked hyperbolic system with a circle
1 Introduction
In this post, we discuss the exponential stability of a networked hyperbolic system with a circle. In many applications, the graphs of these networks contain cycles, such as pipeline networks for gas transportation (see, for example, [1]). In [[2], Page 197], Bastin and Coron mention that certain systems of balance laws exhibit an intrinsic limit of stabilization under local boundary control. Conversely, these systems can be stabilized if L is small.
This finding prompted us to investigate whether a similar phenomenon might also occur in the system we are examining (in a network with a circular structure). As a result, we prove that the system is stabilizable when the arc lengths are sufficiently small. However, if the arc lengths are too large, the system becomes non-stabilizable. To establish the stability result, we perturbed both the arc lengths and the control gain. Additionally, we present some numerical results to illustrate our findings.
2 Modelling
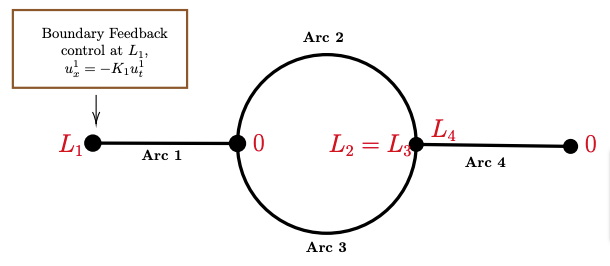
Figure 1: A network with a circle in 4 edges.
We consider a network with a circle and two additional edges. At one boundary node, feedback control action takes place. At the other boundary node, a homogeneous Dirichlet condition is prescribed. For k\in\{1,2,3,4\}, let real numbers c_k>0, \varepsilon_k\ge0 be given. We consider the following system:
\begin{cases} u_{tt}^k=u_{xx}^k-2\varepsilon_ku_t^k-(\varepsilon_k^2-c_k^2)u^k, \quad t\in(0,+\infty),\ x\in[0,L_k],k\in\{1,2,3,4\},\\ u^1(t,0)=u^2(t,0)=u^3(t,0),\\ u^2(t,L_2)=u^3(t,L_3)=u^4(t,L_4),\\ \Sigma_{k=1,2,3}u_x^k(t,0)=0,\\ \Sigma_{k=2,3,4}u_x^k(t,L_k)=0,\\ u^4(t,0)=0,\\ u^1_x(t,L_1)=-K_1u^1_t(t,L_1). \end{cases}
The real number K_1 is the control gain. Besides, the initial state is given:
\begin{cases} U(0,x)=(u^1_0(x),...,u^4_0(x))=(u^1(0,x),...,u^4(0,x)),\\ V(0,x)=(v^1_0(x),...,v^4_0(x))=(u_t^1(0,x),...,u_t^4(0,x)). \end{cases}
3 Main Result
The (not necessarily exponentially) stability of the system is defined follows:
Definition 1
System (1) is stabilizable if there exists a control gain K_1\in\R, such that for all U(0,\cdot)\in\prod\limits_{k=1}^{4}H^1(0,L_k) and all V(0,\cdot)\in\prod\limits_{k=1}^{4}L^2(0,L_k), we have
\lim\limits_{t\rightarrow+\infty}\Vert U(t,\cdot)\Vert_{H^1}=0.
The issue of well-posedness is fundamental to the control problems. By employing classical methods such as the method of characteristics or the theory of strongly continuous one-parameter semigroups of linear operators (see [3]), we can establish the well-posedness of the solution to the system. Building upon the findings in [4] and [5], we identify that the eigenvalue problem of the system (1) corresponds to a Sturm-Liouville eigenvalue problem on the network. Our main result is as follows:
Theorem 1
Assume that c_k=c_1=c,\varepsilon_k=\varepsilon_1=\varepsilon,L_k=L_1=L, that is the length of the arcs in the network and the parameters are the same for all arcs.
• If L \lt L_{min}=\frac{\arctan\sqrt{\frac{2}{7}}}{\sqrt{c^2-\varepsilon^2}}, the system (1) is stabilizable (with \| K_1 \| sufficiently small).
• If L \gt L_{max}=\frac{\pi}{2\sqrt{c^2-\varepsilon^2}}, the system (1) is not stabilizable.
Remark 1
There is still a gap between L_{min} and L_{max}, the idea of eliminating the gap is to analyze all eigenvalues on the imaginary axis for each interval length L. However, on account of the complexity of the characteristic equation, the result cannot be obtained till now.
Perturbation of the arcs L_k
We show that the stability result also holds if the input edge and the output edge have slightly different lengths. For technical reasons, we have to assume that the edges in the cycle are of equal length.
Theorem 2
If K_1=0,L \lt L_{min}, we consider a small perturbation according to L_k\ (k=1,2,3,4) , that is:
\begin{cases} \widetilde{L}_1=L+d_1 r,\\ \widetilde{L}_2=\widetilde{L}_3=L+d_2 r,\\ \widetilde{L}_4=L+d_4 r. \end{cases}
Here d_1,d_2,d_4,r are real constants. The system (1) with c_k=c_1=c,\varepsilon_k=\varepsilon_1=\varepsilon,L_k=\widetilde{L}_k is exponentially stable if |r| is sufficiently small.
Perturbation of control parameter K_1
Also we prove that the system can be stabilized even if K_1\ne0 but sufficiently small.
Theorem 3
The system (1) with c_k=c_1=c,\varepsilon_k=\varepsilon_1=\varepsilon,L_k=L is exponentially stable if L \lt L_{min} and |K_1| is sufficiently small.
For the stability analysis, we employ spectral analysis. For L \lt L_{min}=\frac{\arctan\sqrt{\frac{2}{7}}}{\sqrt{c^2-\varepsilon^2}} with K_1=0 and L_k=L\ (k=1,2,3,4), we first establish the characteristic equation. All the eigenvalues of the system (1) lie in the left half-plane, indicating that the system (1) is L^2-exponentially stable. With the pertubation on the control parameter and the length, the eigenvalue still lie in the left half-plane.
Regarding the instability analysis, our goal is to demonstrate that for sufficiently large edge lengths and for any K_1\in\mathbb{R}, there exists an eigenvalue that lies in the right half-plane. As a consequence, the system (1) with c_k=c_1=c, \varepsilon_k=\varepsilon_1=\varepsilon, and L_k=L_1=L cannot be L^2-exponentially stable.
4 Simulations
Example 1
For the given initial value (3), we can calculate the characteristic function of the system (1). The numerical result generated with MATLAB using the upwind implicit scheme for the system (1), along with the numerical result obtained from the eigenfunctions calculated before, will be shown in the following video.
We take the initial value:
\begin{cases} u^1(0,x)=-4\sin(\frac{\pi}{2}x),\\ u^i(0,x)=2\sin(\frac{\pi}{2}x),\quad i\in\{2,3,4\},\\ u^k_t(0,x)=0,\quad k\in\{1,2,3,4\}. \end{cases}
Video: The time evolution of the network
\varepsilon=\pi,\quad c=\sqrt{1.01}\pi
Green Line: Numerical simulation Result
L=1
Red Line: Exact Solution
Example 2
We normalize the initial L^2 energy as 1.
We take \varepsilon=\pi, c=\sqrt{1.01}\pi. Theorem 1 gives us L_{min}=1.5625,\ L_{max}=5. The time evolution of the log of L^2-energy of the networks with different length of the arcs can be shown in Figure 6.2.1, Figure 6.2.2, and Figure 6.2.3 for K_1=0,1,20. We take the initial value:
\begin{cases} u^1(0,x)=\sin(\frac{\pi x}{L})+\frac{\pi}{L}x,\\ u^2(0,x)=u^3(0,x)=-\sin(\frac{\pi x}{L}),\\ u^4(0,x)=-\frac{2\pi}{L}x,\\ u^k_t(0,x)=0,\quad k\in\{1,2,3,4\}. \end{cases}
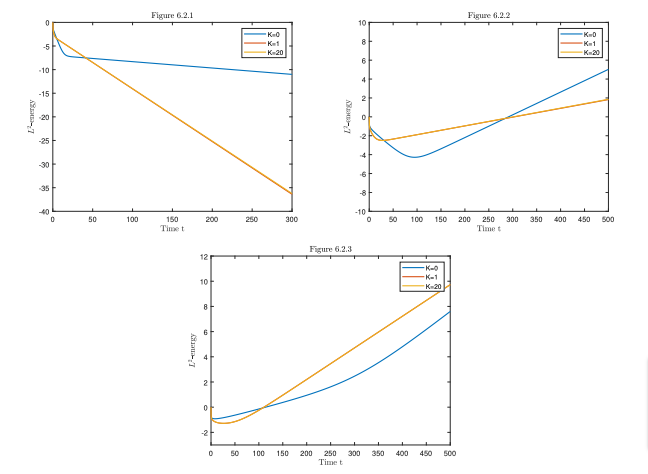
Figure 2. L_1=1 \lt L_{min}\qquad\quad\quad L_2=3\in(L_{min},L_{max})\qquad\quad\quad L_3=6 \gt L_{max}
From the numerical results, we conclude that if there exists a critical length L_c of the arc that divides the stabilization of the system, L_c has a higher probability to be equal to L_{min}.
Example 3
We normalize the initial L^2 energy as 1.
We take \varepsilon=4 and c=5, while L=\frac{1}{2} \gt L_{min}, only if K_1\in(0.8,5.0) can the system possibly be stable. We try to simulate the values of K_1\in{0.9,1,2,3,4,4.5} using the initial value (\ref{in3}). However, because the five lines of the time evolution of L^2-energy of the networks are very close and increasing, we are only presenting the log of energy for K_1=3 in Figure 6.3.1.
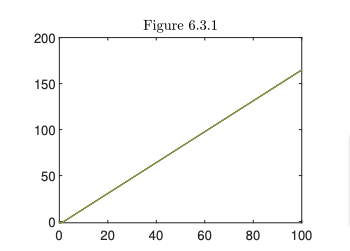
Figure 3. c=5,\ \varepsilon=4,\ L=\frac{1}{2},\ K_1=3
The numerical results show that the system is not exponentially stable even if we cannot theoretically prove it.
5 Conclusion
We studied the stabilization limits of a networked hyperbolic system with a circular structure, governed by a wave equation with nondissipative source terms depending on position and velocity. If the arc lengths are small enough and equal, the system is exponentially stable with a sufficiently small control parameter |K_1|. However, as demonstrated by Bastin and Coron in [2], the system cannot be exponentially stable for any feedback parameters if the arc lengths are sufficiently large. We proved that slightly different arc lengths can still maintain stability.
References
[1] Schmidt, M., Aßmann, D., Burlacu, R., Humpola, J., Joormann, I., Kanelakis, N., Koch, T., Oucherif, D., Pfetsch, M.E., Schewe, L., Schwarz, R., Sirvent, M.: Gaslib—a library of gas network instances (2017) Data, Vol. 2, No. 4, https://doi.org/10.3390/data2040040
[2] Bastin, G., Coron, J.-M.: Stability and Boundary Stabilization of 1-D Hyperbolic Systems (2016) Progress in Nonlinear Differential Equations and their Applications, Vol. 88, p. 307. Birkhäuser/Springer, Subseries in Control. https://doi.org/10.1007/978-3-319-32062-5
[3] Pazy, A.: Semigroups of Linear Operators and Applications to Partial Differential Equations (1983) Applied Mathematical Sciences, Vol. 44, p. 279. Springer. https://doi.org/10.1007/978-1-4612-5561-1 . https://doi.org/10.1007/978-1-4612-5561-1
[4] Below, J.: Sturm-Liouville eigenvalue problems on networks (1988) Math. Methods Appl. Sci., Vol. 10, No. 4, pp. 383–395 https://doi.org/10.1002/mma.1670100404
[5] Below, J., Francois, G.: Spectral asymptotics for the Laplacian under an eigenvalue dependent boundary condition (2005) Bull. Belg. Math. Soc. Simon Stevin, Vol. 12, No. 4, pp. 505–519
|| Go to the Math & Research main page


 Martin Gugat
Martin Gugat Xu Huang
Xu Huang