Michele Spinola
[Past Member] Scientific Assistant (2019 – 2021)
michele.spinola@fau.de
Room 03.315 | DDS – Department of Data Science. FAU DCN-AvH Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship
+49 9131 85-67138
[Past Member] Scientific Assistant (2019 – 2021)
michele.spinola@fau.de
Room 03.315 | DDS – Department of Data Science. FAU DCN-AvH Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship
+49 9131 85-67138
Hello, I am Michele Spinola and I am working as a scientific assistant at the Chair in Applied Analysis Alexander von Humboldt-Professorship at Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) since October 2019. My ongoing doctoral thesis, started in April 2017, is supervised by Prof. Dr. Günter Leugering, head of the Chair in Applied Mathematics 2 (FAU).
My research interests are in the modeling, simulation and optimization of so-called nonlocal population balance equations (PBEs). I am further involved in the teaching of “Mathematics for Engineers” at FAU.
If you have any questions that you want to ask me or remarks that you wish to share with me (e.g. regarding nonlocal PBEs), feel free to contact me.
My posters

Nonlocal Conservation Laws (NLCL) – Modeling, Simulation and Optimal Control
• Alexander Keimer, UC Berkeley • Günter Leugering, Friedrich-Alexander-Universität Erlangen – Nürnberg • Lukas Pflug, Friedrich-Alexander-Universität Erlangen – Nürnberg • ...
My posts on Math and Research
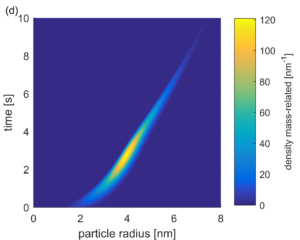
Model-based optimization of ripening processes with feedback modules
Model-based optimization of ripening processes with feedback modules By Michele Spinola 1 Important remark This contribution presents a proof of ...
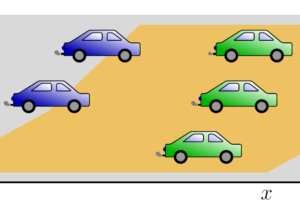
Nonlocal population balance equations and applications
Nonlocal population balance equations and applications By Michele Spinola Motivational example: look ahead behavior of car drivers When analyzing traffic ...
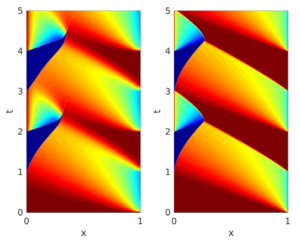
Non-local population balance equations
Non-local population balance equations By Michele Spinola Nichtlokale Populationsbilanzgleichungen. Der Verlauf des Weges wie zur Schule oder zur Arbeit hängt ...