External Research Fellow. Università di Pisa
Friedrich-Alexander-Universität Erlangen-Nürnberg. FAU DCN-AvH Chair for Dynamics, Control, Machine Learning and Numerics – Alexander von Humboldt Professorship.
+49 9131 85-67133
I got my PhD at the FAU DCN-AvH, the Chair for Dynamics, Control, Machine Learning and Numerics at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg.
I am a postdoctoral researcher at Università di Pisa. Previously I have been a postdoc at the “Chaire d’Analyse Mathématique, Calcul des Variations et Équations aux Dérivées Partielles” led by Maria Colombo at EPFL, École Polytechnique Fédérale de Lausanne).
My main research interests lie in the analysis and control of partial differential equations. More specifically, I’ve been working on the following topics: conservation laws; transport with rough velocity fields; flows on networks; local and nonlocal (degenerate higher-order) parabolic PDEs; free boundary problems; variational and topological methods for the study of nonlinear problems.
PhD Thesis: Analysis, control, and singular limits for hyperbolic conservation laws (July 24, 2023)
Events
• MLPDEs 2026 (June 22-24, 2026): Machine Learning and PDEs Workshop, Erlangen – Bavaria, Germany.
• MLPDEs 2025 (April 28-30, 2025): Machine Learning and PDEs Workshop, Erlangen – Bavaria, Germany.
• September 20, 2024 FAU DCN-AvH Seminar: “Optimal Regularity for the 2D Euler Equations in the Yudovich class”
• July 24, 2023 PhD defense: “Analysis, control, and singular limits for hyperbolic conservation laws”
Projects
• TRR154
My posters

The Singular limit of Nonlocal conservation Laws to Local Conservation Laws
Teaching
• WS 22/23: Transport Phenomena
• WS 22/23: Mathematical Modeling in the Life Sciences
• WS 21/22: Modeling and Analysis in Continuum Mechanics 1
• WS 21/22: Transport Phenomena
My posts on Math & Research
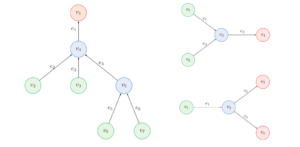
Control of Advection-Diffusion Equations on Networks and Singular Limits

Flows on Networks
Publications
2025
- , , , , :
Control of Hyperbolic and Parabolic Equations on Networks and Singular limits
In: Vol 15, No. 1, Mathematical Control and Related Fields, 2025, p. 348-389
DOI: 10.3934/mcrf.2024015
URL: https://hal.science/hal-03233211
BibTeX: Download - , , :
Pointwise constraints for scalar conservation laws with positive wave velocity
In: Zeitschrift für Angewandte Mathematik und Physik 76 (2025), Article No.: 111
ISSN: 0044-2275
DOI: 10.1007/s00033-025-02459-0
BibTeX: Download
2024
- , , , , , , , :
Oleinik-type estimates for nonlocal conservation laws and applications to the nonlocal-to-local limit
In: Journal of Hyperbolic Differential Equations 21 (2024), p. 681-705
ISSN: 0219-8916
DOI: 10.1142/S021989162440006X
BibTeX: Download - , , , , :
Exponential convergence to steady-states for trajectories of a damped dynamical system modeling adhesive strings
In: Mathematical Models & Methods in Applied Sciences (2024)
ISSN: 0218-2025
DOI: 10.1142/S021820252450026X
BibTeX: Download - , :
Fractional Hardy–Rellich inequalities via integration by parts
In: Nonlinear Analysis - Theory Methods & Applications 243 (2024), Article No.: 113478
ISSN: 0362-546X
DOI: 10.1016/j.na.2023.113478
BibTeX: Download - , :
INTERFACE PROPAGATION PROPERTIES FOR A NONLOCAL THIN-FILM EQUATION
In: SIAM Journal on Mathematical Analysis 56 (2024), p. 173-196
ISSN: 0036-1410
DOI: 10.1137/22M1510297
BibTeX: Download
2023
- , , , , :
A general result on the approximation of local conservation laws by nonlocal conservation laws: The singular limit problem for exponential kernels
In: Annales de l'Institut Henri Poincaré - Analyse Non Linéaire 40 (2023), p. 1205-1223
ISSN: 0294-1449
DOI: 10.4171/AIHPC/58
BibTeX: Download - , , , , :
Long-time convergence of a nonlocal Burgers' equation towards the local N-wave
In: Nonlinearity (2023)
ISSN: 0951-7715
DOI: 10.1088/1361-6544/acf01d
URL: https://iopscience.iop.org/article/10.1088/1361-6544/acf01d
BibTeX: Download - , :
Critical functions and blow-up asymptotics for the fractional Brezis-Nirenberg problem in low dimension
In: Calculus of Variations and Partial Differential Equations 62 (2023)
ISSN: 0944-2669
DOI: 10.1007/s00526-023-02446-1
BibTeX: Download - , :
Stability with explicit constants of the critical points of the fractional Sobolev inequality and applications to fast diffusion
In: Journal of Functional Analysis 285 (2023), Article No.: 110093
ISSN: 0022-1236
DOI: 10.1016/j.jfa.2023.110093
BibTeX: Download - , :
On the Controllability of Entropy Solutions of Scalar Conservation Laws at a Junction via Lyapunov Methods
In: Vietnam Journal of Mathematics (2023)
ISSN: 0866-7179
DOI: 10.1007/s10013-022-00598-9
BibTeX: Download
2022
- , :
Differentiability in Measure of the Flow Associated with a Nearly Incompressible BV Vector Field
In: Archive for Rational Mechanics and Analysis (2022)
ISSN: 0003-9527
DOI: 10.1007/s00205-022-01820-1
BibTeX: Download - , , , :
On existence and uniqueness of weak solutions to nonlocal conservation laws with BV kernels
In: Zeitschrift für Angewandte Mathematik und Physik 73 (2022), Article No.: 241
ISSN: 0044-2275
DOI: 10.1007/s00033-022-01766-0
BibTeX: Download - , :
Sharp criteria for the waiting time phenomenon in solutions to the thin-film equation
In: Communications in Partial Differential Equations (2022)
ISSN: 0360-5302
DOI: 10.1080/03605302.2022.2056702
BibTeX: Download - , , :
On Liouville-type theorems for the 2D stationary MHD equations
In: Nonlinearity 35 (2022), p. 870-888
ISSN: 0951-7715
DOI: 10.1088/1361-6544/ac3f8b
BibTeX: Download
2021
- , , , , :
Boundary Controllability and Asymptotic Stabilization of a Nonlocal Traffic Flow Model
In: Vietnam Journal of Mathematics (2021)
ISSN: 0866-7179
DOI: 10.1007/s10013-021-00506-7
BibTeX: Download - , , , :
Vanishing viscosity for a 2 x 2 system modeling congested vehicular traffic
In: Networks and Heterogeneous Media 16 (2021), p. 413-426
ISSN: 1556-1801
DOI: 10.3934/nhm.2021011
BibTeX: Download - , , , :
Singular limits with vanishing viscosity for nonlocal conservation laws
In: Nonlinear Analysis - Theory Methods & Applications (2021)
ISSN: 0362-546X
DOI: 10.1016/j.na.2021.112370
BibTeX: Download - , , , :
Singular limits with vanishing viscosity for nonlocal conservation laws
In: Nonlinear Analysis - Theory Methods & Applications 211 (2021), Article No.: 112370
ISSN: 0362-546X
DOI: 10.1016/j.na.2021.112370
BibTeX: Download