Author: Alexei Gazca, FAU DCN-AvH
Code: ![]()
Below is a description of the types of problems that can be tackled using the code contained in this repository.
Solving linear systems arising from the discretisation of partial differential equations can be an extremely challenging and computationally intensive task, especially for problems posed in more than two spatial dimensions: employing iterative methods is usually a must.
An important observation one can make is that the number of iterations required to solve a problem will typically grow as the mesh is refined. Multigrid methods can be used to deal with this issue: it can be shown for instance that the standard multigrid method leads to mesh-independent convergence when applied to a discretisation of the Laplace problem.
In this work we are interested in the numerical approximation of incompressible flow. The most basic problem in this setting is the Stokes system posed on a domain \Omega\subset \R^d.
\begin{aligned} -div( 2\nu_* \bm{D}(\vec{u})) + \nabla p = \bm{f}\qquad &\text{in }\Omega,\\ div \vec{u} = 0\qquad &\text{in }\Omega, \end{aligned} (1)
where \vec{u}\colon \Omega \to \R^d is the velocity, p\colon \Omega \to \R is the pressure, and \nu_*>0 and \bm{f}\colon \Omega \to \R^d are the given viscosity and body force, respectively. When solving the linear system that arises from a finite element discretisation, the following modification of the operator acting on the velocity brings certain advantages:
2\nu_* \bm{D}(\vec{u}) \mapsto 2\nu_*\bm{D}(\vec{u}) + \gamma \nabla (div \vec{u}) \qquad \gamma >0.
In particular, when the parameter \gamma is large the approximation of the Schur complement becomes straightforward (note also that this modification does not change the solution). Block preconditioners that employ this strategy are referred to as augmented Lagrangian preconditioners.
One of the drawbacks of the augmented Lagrangian approach is that the standard multigrid algorithm ceases to be effective when applied to the modified velocity operator; the main difficulty is that the operator degenerates as \gamma increases. A specialised multigrid algorithm is therefore needed.
The first ingredient of a robust multigrid method is a robust relaxation scheme; many smoothers in multigrid can be framed in terms of a subspace decomposition V^h = \sum_k V^h_k, where one solves the problem in each subspace V^h_k and then combines the updates (e.g.\ in a Jacobi relaxation each subspace V^h_k is defined as the linear span of a single basis function \phi^h_k). It is now well understood that for problems with the structure described above one can obtain a robust relaxation by employing a space decomposition that “captures the kernel” of the semidefinite operator:
\mathrm{ker}(div) = \sum_k \mathrm{ker}(div) \cap V^h_k, (2)
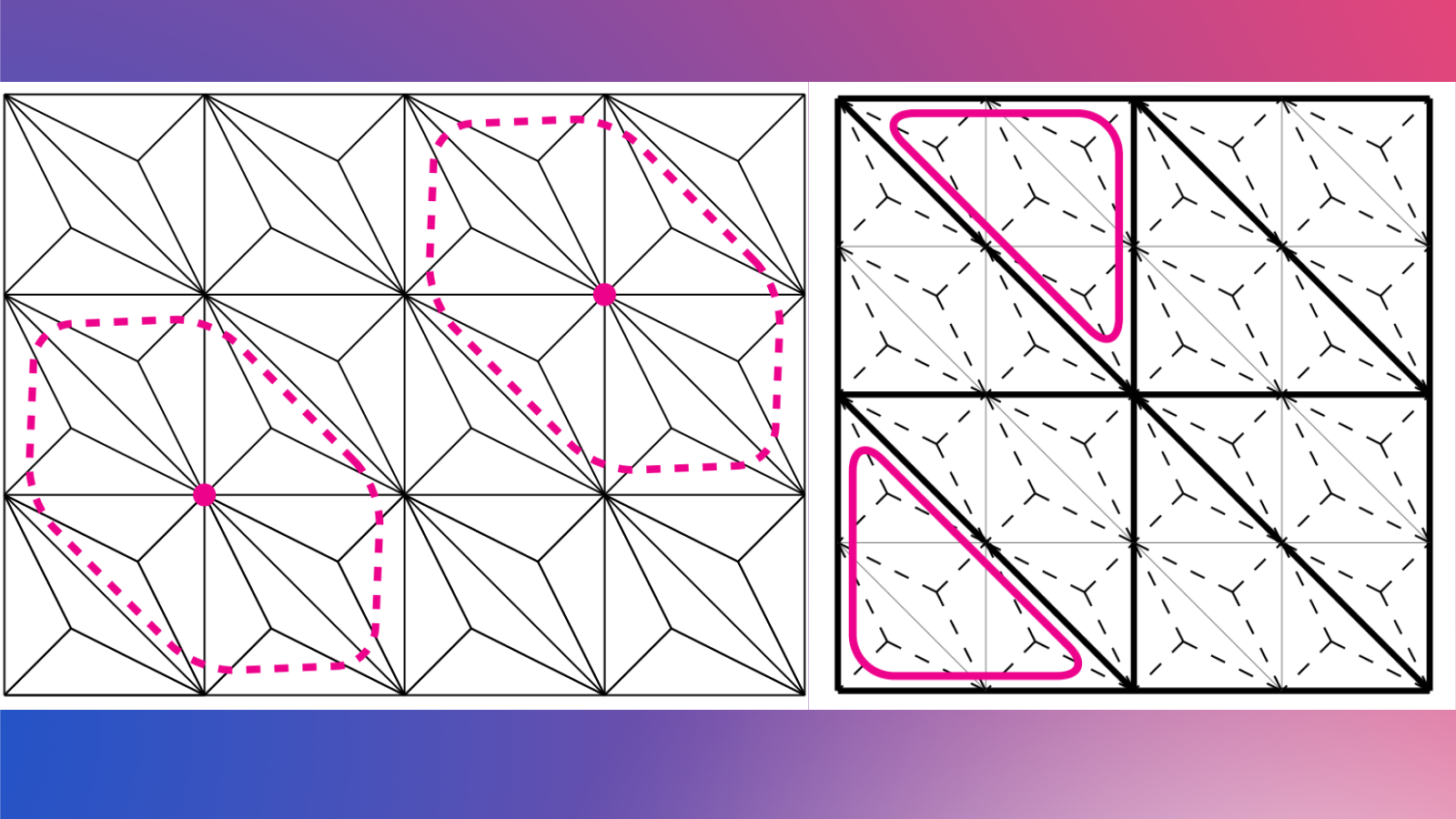
which means that the decomposition must be in some sense sufficiently rich to capture elements in the kernel, and e.g.\ the Jacobi relaxation cannot satisfy this requirement. The present work is mostly based on a Scott-Vogelius discretisation for the velocity and pressure, in which case a kernel capturing decomposition can be obtained if one defines the subspaces as the linear span of the functions supported on “Macrostar” patches (see Figure 1).
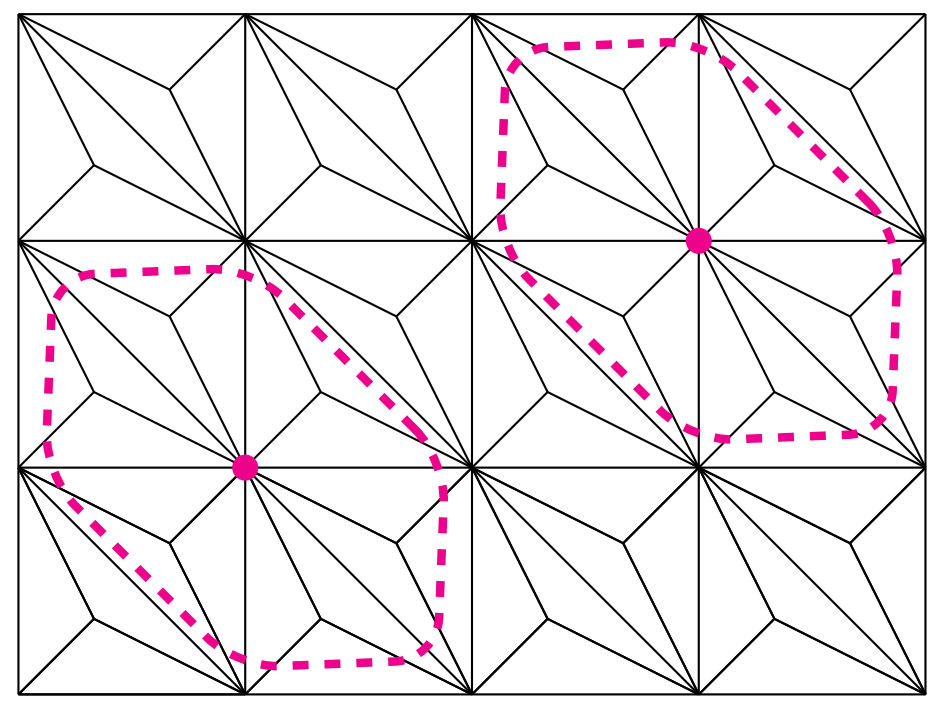
Figure 1. Macrostar patches on a barycentrically refined mesh in two dimensions.
The second ingredient of a robust multigrid method are robust transfer operators. It is now known that a requirement of a robust prolongation operator is stability with respect to the energy norm; this could be an issue if one applies a standard prolongation operator based on interpolation to a problem where \gamma is large (since divergence-free functions on the coarse mesh are mapped to functions on the fine mesh that do not necessarily have zero divergence). For a Scott–Vogelius discretisation one can modify the standard prolongation operator by adding a “correction” that is computed by solving Stokes-like problems on the coarse macroelements (see Figure 2)
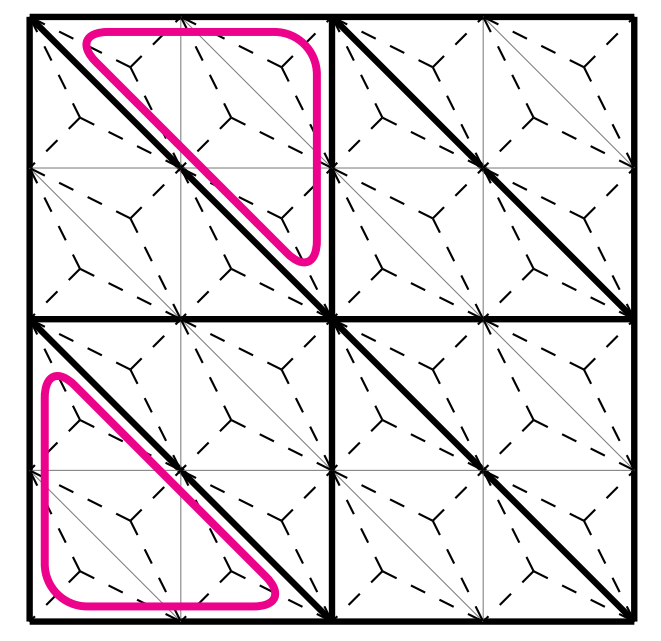
Figure 2. The correction to the prolongation operator is computed on the coarse macroelements.
The code developed here builds upon work contained in this repository; there, the ideas described above were used to obtain robust preconditioners for the incompressible Navier–Stokes system.
For more information, see:
[1] P. E. Farrell, L. Mitchell, and F. Wechsung. An augmented Lagrangian preconditioner for the 3D stationary incompressible Navier–Stokes equations at high Reynolds number. SIAM J. Sci. Comput., 41(5):A3073-A3096, 2019
This project is an extension of the works mentioned above to the non-Newtonian setting with potentially implicit constitutive relations (in which the formulation includes the stress); thermal effects can also be incorporated by coupling the system to an equation for the temperature; further extensions to other settings/discretisations are the subject of current research. For a detailed description see:
[3] P. E. Farrell, and P. A. Gazca-Orozco. An augmented Lagrangian preconditioner for implicitly constituted non-Newtonian incompressible flow. SIAM J. Sci. Comput., 42(6):B1329-B1349, 2020
|| Go to the Math & Research main page