Evaluating client contribution in Federated learning

In the recent years federated learning has emerged as a powerful paradigm for training machine learning models across decentralized data sources, enabling collaborative intelligence without compromising data privacy. In this post, which follows a great introduction by Ziqi Wang on the topic of Federated learning, I address the specific issue of client contribution evaluation in greater detail.

1 What is client contribution and why do we need it?

As mentioned previously, in the federated learning the data is distributed between $n$ clients. In practice the data between the clients is not generated following an independent and identical distribution (i.i.d.). For example, hospitals located in different areas will get a different type of patients, since the respective population of these areas is different. This heterogeneity of the data is one of the main topics of study in the federated learning algorithms. Client contribution evaluation aims to quantify the usefulness of each client’s data for model training. A key challenge is identifying which clients hold higher-quality data — that is, data that contributes more effectively to improving the global model. One of the main tools for client contribution evaluation is the concept from the cooperative game theory: the Shapely Value.

2 Shapely value

A cooperative game with transferable utility (TU) is defined as a pair $(N, v)$ , where:
• $N = \{1, 2, \dots, n\}$ is a finite set of players,
• $v : \mathcal{P}(N) \rightarrow \mathbb{R}$ is the utility function, satisfying $v(\emptyset) = 0$ ,
• For each coalition (subset) $S \subseteq N$ , the value $v(S)$ represents the total utility that coalition $S$ achieves.

A central concept in TU games is the payoff vector $\varphi \in \mathbb{R}^N$ , which specifies how the total utility $v(S)$ obtained by a coalition $S$ is distributed among its members. The design and analysis of such payoff allocations are fundamental to understanding fairness, stability, and incentives in cooperative scenarios.

In our particular case of federated learning we can use $N$ the set of all the clients and $v$ the accuracy achieved by the model (trained using the combination of these clients) on an evaluation dataset.

It is quiet natural to look for a payoff vector $\phi$ such that the four following properties are verified:
• Efficiency: The sum of the payoffs equals to the total value, i.e.

$\sum_{i \in N} \phi_i(v) = v(N).$

• Symmetry: If two players, $i$ and $j$ , contribute equally to the value of any coalition, then their Shapley values are equal, i.e.

$\forall i, j \in N, (\forall S \subseteq N\{i,j \}, v(S\cup i)=v(S \cup j)) \implies \phi_i(v)=\phi_j(v).$

• Linearity: For any two utility functions $v$ and $w$ and scalar $\lambda$ ,

$\phi_i(v + \lambda w) = \phi_i(v) + \lambda \phi_i(w).$

• Null player: If a player doesn’t contribute to any coalition he is not getting a reward, ie

$\forall i\in N, [\forall S \subset N - \{i\}, U(S)=U(S \cup \{i\})] \implies \phi_i(U)=0.$

It can be shown that there exists a unique payoff vector which simultaneously verifies these 4 properties. It is called Shapely value (SV) [3] and can be defined by the following formula:

$\phi_i(v) = \sum_{S \subseteq N \setminus \{i\}} \frac{|S|! (|N| - |S| - 1)!}{|N|!} (v(S \cup \{i\}) - v(S))$

or equivalently by

$\phi_i(v) = \frac{1}{n!} \sum_{\pi \in \mathfrak{S}_N} \left[ v(\text{Pre}_i^\pi \cup \{i\}) - v(\text{Pre}_i^\pi) \right],$

where $\text{Pre}_i^\pi$ is the set of the indices $j$ such that their image by $\pi$ is smaller than $i$ , i.e.
$\text{Pre}_i^\pi:= \{j \in N |\pi(j) \lt \pi(i) \}$ .

As an attentive reader may have noticed, computing the (SV) is exponentially expensive depending on the number of clients. Even more, given that in order to compute $v(S)$ for a given coalition $S$ it is necessary to retrain the model from scratch which may give significantly different results depending on the order in which the clients are chosen and is very computationally costly.

First step in solving this issue is to decompose the utility function as a sum of smaller ones [5]:

$v:=\sum_{t=1}^T v^t,$

where $v^t$ is the accuracy gain made in the round number $t$ . When the linearity of the (SV) allows to write $\phi(v)=\sum_t \phi(v^t).$ A panoply of different (mostly Monte Carlo based) methods then allow to estimate -more or less efficiently- the (SV) of each local utility function [1][4]. This is an active field of research that will not be addressed in greater detail in this post.

3 ShapleyFL

3.1 Algorithm

In this section I would like to present how Shapely value can be used to improve the robustness of the federated learning training. The idea is simple: during the classic Federated Average algorithm [2] presented in one of the previous posts the server may change the weights of the clients according to their (SV). This gives the following algorithm:

Algorithm 1

. Federated Averaging with Shapeley updates
Require: Number of clients $K$ , learning rate $\eta$ , initial global model $w_0$ , weights of the clients $(\alpha_k)_{k\in [K]}$

1: for each round $t = 1, 2, \dots, T$ do
2: Server selects a subset $\mathcal{C}_t \subseteq \{1, \dots, K\}$ of clients
3: for each client $k \in \mathcal{C}_t$ in parallel do
4: Client $k$ receives current model $w_t$

5: Client $k$ updates model locally via SGD:

$w_{t+1}^k \leftarrow \text{SGD}_k(w_t, \eta)$

6: Client $k$ sends $w_{t+1}^k$ to server
7: end for
8: Server updates the weights:

$\alpha \leftarrow \alpha + \phi^t \in \mathbb{R}^K$

Where $\phi^t$ is the estimate of the (SV)
9: Server aggregates updates:

$w_{t+1} \leftarrow \sum_{k \in \mathcal{C}_t} \frac{\max(\alpha_k,0)}{A} w_{t+1}^k$

where $A$ is the normalization term defined by $A=\sum_k \max(\alpha_k,0)$ .
10: end for

An Illustration

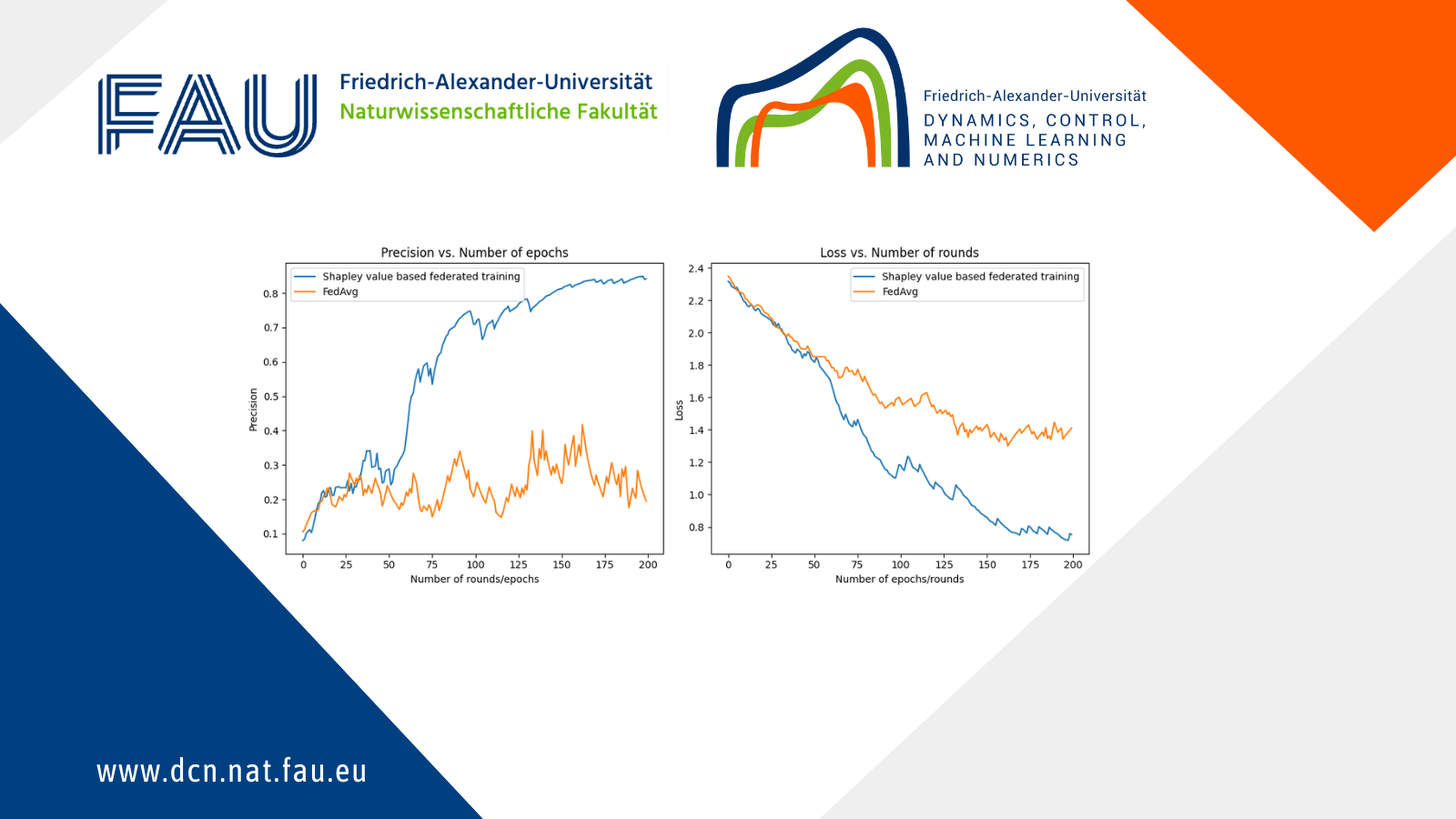
To illustrate the advantages of this algorithm, let us consider a toy example of MNIST dataset based federated learning experience with 9 clients. Among these clients 5 have decided to sabotage the training and all agreed to apply the same permutation (with no fixed points) to their labels. In this case the classic FedAvg will not be able to consistently attain a more than 50 percent accuracy (since more than the half of the clients are lying).

At each round only 3 clients are called for computational reasons.

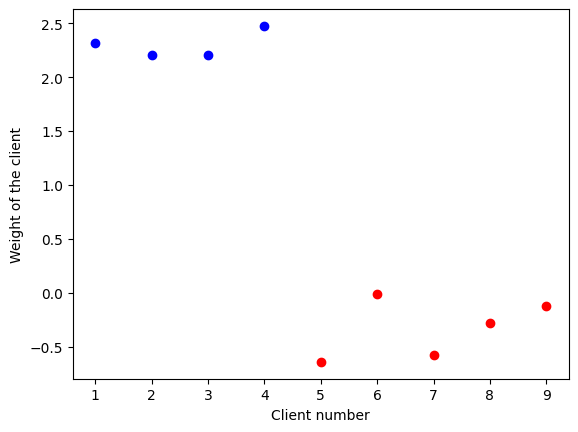
Figure 1. The weights of the clients in (SV) based method at the end of the training

However the (SV) based algorithm is able to “identify” the liars (red points in the first figure) and achieve a much better performance (cf Figure 2).

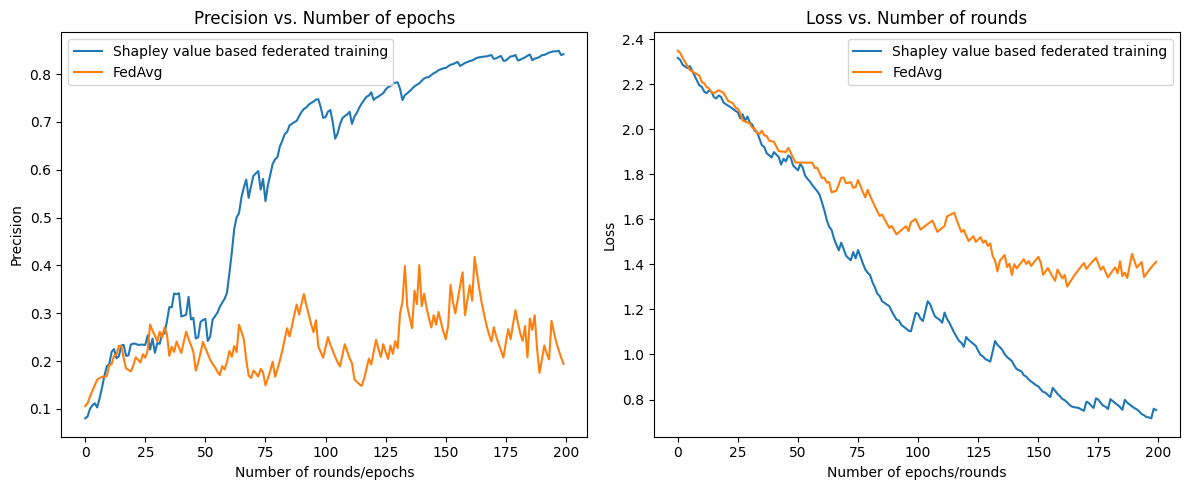
Figure 2. The performance under a data injection attack

4 Challenges

Despite their remarkable efficiency for robust Federated Learning training, accuracy based (SV) estimates remain computationally expensive and the different methods to optimize these calculations remain an active field of research. Another related topic studied in our chair is the use of the (SV) for more incentive in Federated Learning.

References

[1] R. Jia, D. Dao, B. Wang, F. Ann Hubis, N. Hynes, N.M. Gurel, B. Li, C. Zhang, D. Song, C. Spanos (2023) Towards Efficient Data Valuation Based on the Shapley Value, arXiv:1902.10275
[2] B. McMahan, E. Moore, D. Ramage, S. Hampson, B. Aguera y Arcas (2017) Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, pages 1273–1282. PMLR, ISSN: 2640-3498
[3] L.S. Shapley (1951) Notes on the N-Person Game — II: The Value of an N-Person Game. Technical report
[4] G. Wang, C.X. Dang, Z. Zhou (2019) Measure Contribution of Participants in Federated Learning, arXiv:1909.08525
[5] T. Wang, J. Rausch, C. Zhang, R. Jia, D. Song (2020) A Principled Approach to Data Valuation for Federated Learning, arXiv:2009.06192