Author: Carlos Esteve, Deusto CCM
Code: ![]()
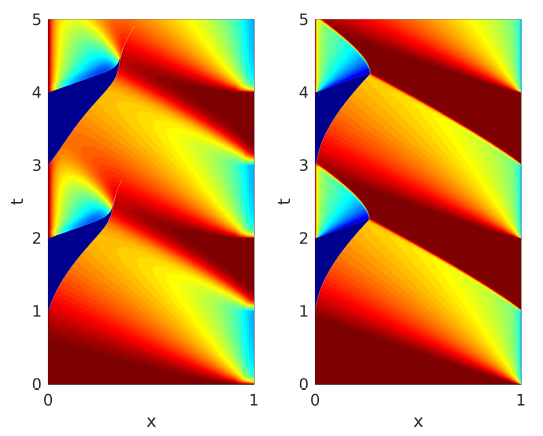
In a previous post “Inverse Design For Hamilton-Jacobi Equations“, described all the possible initial states that agree with the given observation of the system at time T>0T>0 on the reconstruction of the initial state in many evolution models.
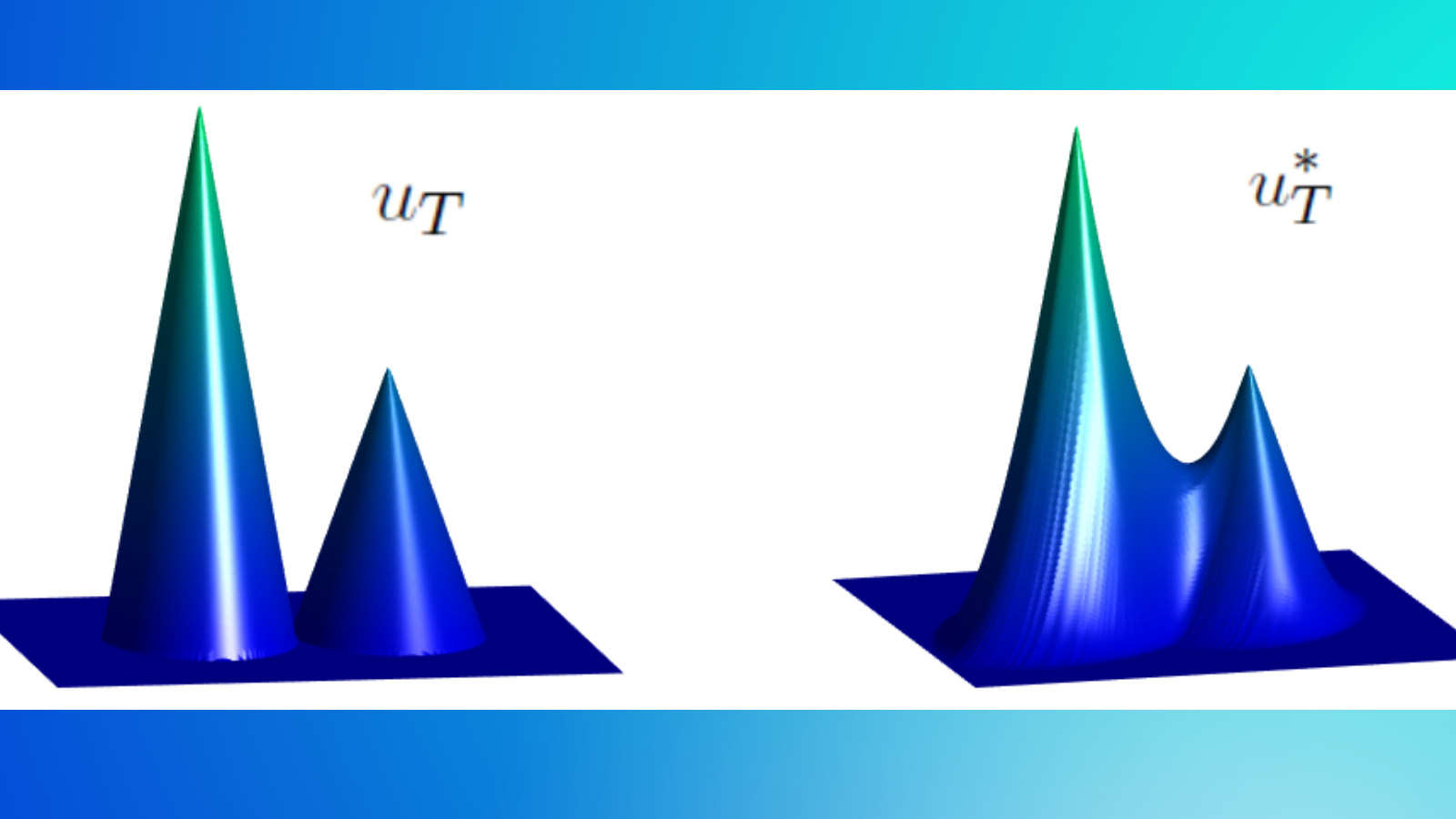
Our goal here is to study the inverse design problem associated to Hamilton Jacobi Equations (HJ). More precisely, for a given target function u_T and a time horizon T>0, we want to construct all the initial conditions u_0 such that the viscosity solution of (HJ) coincides with u_T at time T.
The study of this problem can also be motivated by considering the following question:
Given an observation of the solution to (HJ) at time T>0, can we construct all the possible initial data that agree we the observation at time T?
For this purpose, for a fixed T>0
, we define the following nonlinear operator, which associates to any initial condition u0, the function u(T,⋅), where u is the viscosity solution of (HJ):
\mathbb{S}^{+}_{T}:C^{0,1}(\mathbb{R}^n) \rightarrow C^{0,1}(\mathbb{R}^n) \\
u_0 \longmapsto S^+_{T} u_0= u(\mathbb{T}, \cdot )
The inverse design problem that we are considering is then reduced to, for u_T and T>0 given, characterize all the initial conditions u_0 satisfying S^+_{T} u_0= u(\mathbb{T}, \cdot ) .
|| Go to the Math & Research main page