Postdoctoral Researcher
Funded by Alexander von Humboldt Foundation
ilias.ftouhi@fau.de
Room 03.315 | Friedrich-Alexander-Universität Erlangen-Nürnberg. FAU DCN-AvH Chair for Dynamics, Control, Machine Learning and Numerics – Alexander von Humboldt Professorship.
+49 9131 85-67138
I am Ilias Ftouhi. I defended my PhD at Sorbonne University in Paris in 2021 under the supervision of Professors Jimmy Lamboley and Antoine Henrot.
I am currently an Alexander von Humboldt postdoctoral researcher hosted by the Chair for Dynamics, Control, Machine Learning and Numerics.
I am interested in theoretical and numerical study of shape optimization problems and the use of deep learning techniques in solving inverse problems.
PhD Thesis: Blaschke-Santaló diagrams and other shape optimization problems (January 2021)
PhD Thesis: PhD Thesis (Slides)
Events
• October 7-10, 2024 CIN-PDE 2024 Poster: Optimal Shape Design and Placement of Sensors via a Geometric Approach (Ilias Ftouhi, Enrique Zuazua) | see poster. Conference on Control, Inversion and Numerics for PDEs (October 7-10, 2024 at Fudan University, Shanghai)
• Introduction to shape optimization and some relevant problems Feb. 01, 2024
• Long Night of Sciences (NdW23) Optimale Steuerung einer Schafherde Oct. 01, 2023
• FAU DCN-AvH Workshop, Blaschke-Santaló diagrams in spectral geometry Oct. 01, 2021
My posts
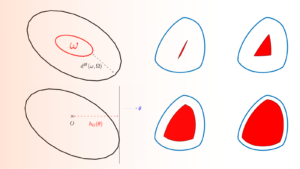
Using the support function for optimal shape design
My posters
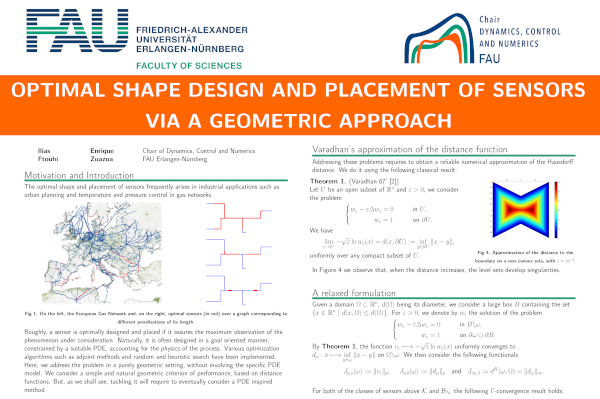
Optimal shape design of sensors via a geometric approach
Sharp estimates for the cheeger constant in the planar case
Publications
2025
- :
Improved Description of Blaschke–Santaló Diagrams via Numerical Shape Optimization
In: Applied Mathematics and Optimization 91 (2025), Article No.: 55
ISSN: 0095-4616
DOI: 10.1007/s00245-025-10250-w
BibTeX: Download - :
The Monotonicity of the Cheeger constant for Parallel Bodies
In: Journal of Optimization Theory and Applications 206 (2025), Article No.: 44
ISSN: 0022-3239
DOI: 10.1007/s10957-025-02727-z
BibTeX: Download - Zakaria F, Ftouhi I, Zuazua E:
Optimal L^p-approximation of convex sets by convex subsets
(2025)
Open Access: https://arxiv.org/pdf/2501.00928
BibTeX: Download
2024
- , , :
Sharp inequalities involving the Cheeger constant of planar convex sets
In: Esaim-Control Optimisation and Calculus of Variations 30 (2024), Article No.: 23
ISSN: 1262-3377
DOI: 10.1051/cocv/2024015
BibTeX: Download - , :
Optimal Placement and Shape Design of Sensors via Geometric Criteria
2024 European Control Conference, ECC 2024 (Stockholm, SWE, June 25, 2024 - June 28, 2024)
In: 2024 European Control Conference, ECC 2024, Stockholm, Sweden: 2024
DOI: 10.23919/ECC64448.2024.10591236
BibTeX: Download
2023
- , :
Optimal design of sensors via geometric criteria
In: Journal of Geometric Analysis 33 (2023)
ISSN: 1050-6926
DOI: 10.1007/s12220-023-01301-1
URL: https://link.springer.com/article/10.1007/s12220-023-01301-1
BibTeX: Download
2022
- :
Complete systems of inequalities relating the perimeter, the area and the Cheeger constant of planar domains
In: Communications in Contemporary Mathematics (2022)
ISSN: 0219-1997
DOI: 10.1142/S0219199722500547
BibTeX: Download - :
On a Pólya's inequality for planar convex sets
In: Comptes Rendus Mathematique 360 (2022), p. 241-246
ISSN: 1631-073X
DOI: 10.5802/crmath.292
BibTeX: Download - :
WHERE TO PLACE A SPHERICAL OBSTACLE SO AS TO MAXIMIZE THE FIRST NONZERO STEKLOV EIGENVALUE
In: Esaim-Control Optimisation and Calculus of Variations 28 (2022)
ISSN: 1292-8119
DOI: 10.1051/cocv/2021109
BibTeX: Download - , :
The diagram (λ 1 , µ 1 )
In: Mathematical Reports (2022)
ISSN: 1582-3067
Open Access: http://imar.ro/journals/Mathematical_Reports/Pdfs/2022/1-2/9.pdf
URL: http://imar.ro/journals/Mathematical_Reports/Pdfs/2022/1-2/9.pdf
BibTeX: Download - , :
THE DIAGRAM (λ1, μ1)
In: Mathematical Reports 24(74) (2022), p. 159-177
ISSN: 1582-3067
URL: http://imar.ro/journals/Mathematical_Reports/Pdfs/2022/1-2/9.pdf
BibTeX: Download
2021
- :
On the Cheeger inequality for convex sets
In: Journal of Mathematical Analysis and Applications (2021)
ISSN: 0022-247X
DOI: 10.1016/j.jmaa.2021.125443
URL: https://hal.science/hal-03006015/document
BibTeX: Download - , :
Blaschke–Santaló diagram for volume, perimeter and first Dirichlet eigenvalue.
In: SIAM Journal on Mathematical Analysis (2021)
ISSN: 0036-1410
DOI: 10.1137/20M1345396
URL: https://hal.science/hal-02850711v2/document
BibTeX: Download
