Convexity and Starshapedness of feasible sets in Stationary Flow Networks

This research was funded by DFG in the SFB Transregio 154: Mathematical modelling, simulation and optimization using the example of gas networks.

Uncertainty often plays an important role in application driven modeling. This often leads to optimization problems with probabilistic constraint. The main task insolving probabilistic constraint optimization problems is to compute the probabilistic constraint. The probabilistic constraint often has the form

$\mathbb{P}(\ \zeta \in M\ ),$

where $\zeta$ is a realization of some random variable and $M$ is the feasible set. The feasible set in our context are all stationary states in a gas network, for which the gas pressure satisfies box constraints at the network junctions. For computing this probability, we use the spheric radial decomposition (SRD) for Gaussian distributed random variables with zero mean and correlation $R$ :

$\mathbb{P}(\ \zeta \in M(x)\ ) = \int_{\mathbb{S}^{n-1}} \mu_\chi \{\ r \geq 0\ \vert\ r L v \in M\ \}\ d\mu_\eta(v).$

Here, $\mathbb{S}^{n-1}$ is the $(n-1)$ -dimensional unit sphere in $\mathbb{R}^n$ , $\mu_\eta$ is the uniform distribution, $\mu_\chi$ denotes the $\chi$ -distribution with $p$ degrees of freedom and $L$ is such that $R = L L^\top$ .

The one-dimensional sets $\{\ r \geq 0\ \vert\ r L v \in M\ \}$ can be represented as union of disjoint intervals. For an algorithmic solution of the probabilistic constraint, a lot of knowledge of the feasible set $M$ is necessary.

In [1], we analyze the feasible set for convexity and star-shapedness since then the one-dimensional sets $\{\ r \geq 0\ \vert\ r L v \in M\ \}$ are just intervals and can be computed much faster.

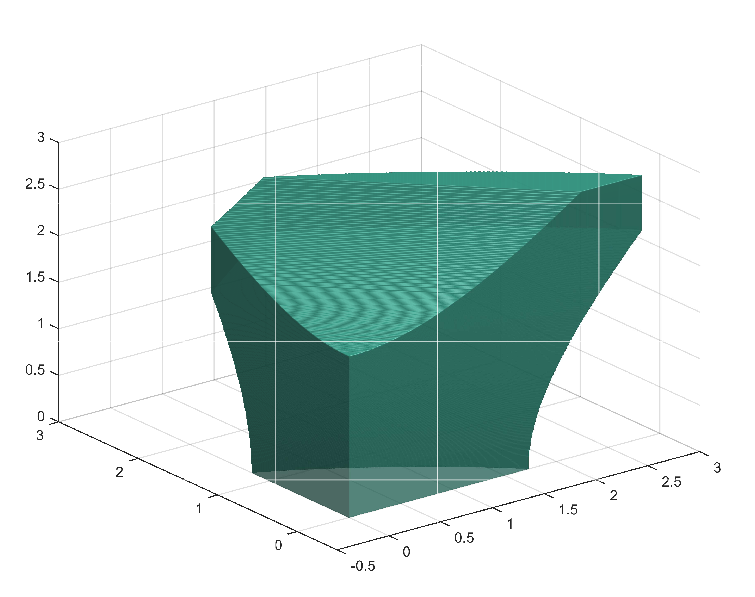
A main assumption for both, convexity and star-shapedness is, that all upper pressure bounds are larger or equal to all lower pressure bounds. In Figure 1, we show some results for a linear graph with two edges and in Figure 2, we show some results for a tree-structured graph with two edges.

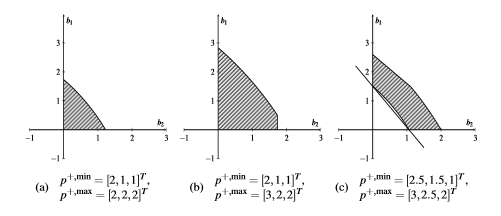Figure 1. Feasible sets for different pressure bounds on a linear graph

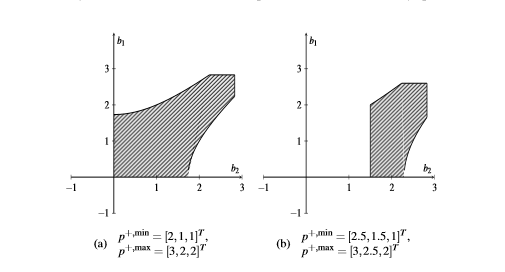Figure 2. Feasible sets for different pressure bounds on a tree-structured graph

References

[1] M. Gugat, R. Schultz, M. Schuster, Convexity and Starshapedness of Feasible Sets in Stationary Flow Networks, Netw. Heterog. Media, 15(2), 171-195, 2020