Breaking the symmetry with Robin boundary conditions

By Alba Lia Masiello, Visiting PhD student from University of Naples Federico II

Introduction

Establishing symmetry properties of solutions to differential equations is a very important task in mathematical analysis, both from the theoretical point of view and for applications. Indeed, partial differential equations arise in modeling many phenomena in physics, mechanics, and so on.

A first question that arises quite naturally is whether the solution to a PDE on a given domain $\Omega\subset \R^n$ might reflect the symmetry of the domain. A positive answer to this question would allow us to numerically solve the PDE more easily and in a more efficient way.

For instance, if we consider

$\begin{cases} -\Delta u= f(u) & \text{in } \Omega,\\ u=0 & \text{on } \partial\Omega, \end{cases} (1)$

where $\Omega$ is symmetric with respect to the $x_1$ axis, is it true that

$u(x_1,\dots, x_n)=u(-x_1,\dots, x_n)?$

If we do not require extra assumptions on the functions $f$ and $u$ , the answer to this question is no. A very well-known example is the following. Let $B$ be the unitary ball in $\R^n$ , let us consider the eigenvalues problem on $B$

$\begin{cases} -\Delta u= \lambda u & \text{in } B,\\ u=0 & \text{on } \partial B. \end{cases} (2)$

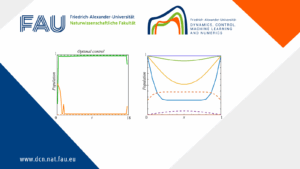
Even if the ball is symmetric with respect to every line containing its center, it is not true that every eigenfunction (i.e. every non-identically zero solution to (2)) shares the same property, as one can see in Figure 1.

Figure 1. The level sets of the first and the second eigenfunction of the Laplacian on $B$

The first eigenfunction, that is to say, the one associated with the lowest $\lambda$ for which there exists a non-zero solution to (2), is radial, while the second one is not. A first difference between these two eigenfunctions is that the first one has constant sign, while the second is a sign-changing function.

In the context of positive solutions to (1), Gidas, Ni, and Nirenberg, in the celebrated paper [3], were able to prove the radial symmetry of solutions when $\Omega$ is a ball.

Theorem 1.
Let $f=f_1+f_2$ , where $f_1$ is a locally Lipschitz function and $f_2$ is non-decreasing. Then, any positive solution $u\in C^2(B)$ to (1) has to be radial (and decreasing along the radii).

The main tool in proving this result is the moving plane method, first adopted by Aleksandrov in the context of differential geometry [1], and then by Serrin [4] in the context of PDEs.

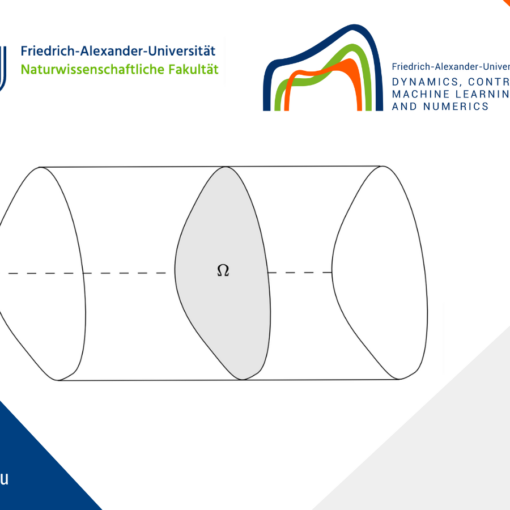
Briefly, it works as follows. Let us consider an hyperplane $H_\lambda=\{x\in \R^n : x\cdot e=\lambda\}$ , whose normal has the same direction as $e\in\R^n.$ We move the hyperplane $H_\lambda$ from a minimal position ( $H_\lambda\cap \Omega=\emptyset$ ) to a maximal one, until the reflected cap $\Sigma'(\lambda)$ with respect to $H_\lambda$ lies in $B$ , (see Figure 2)

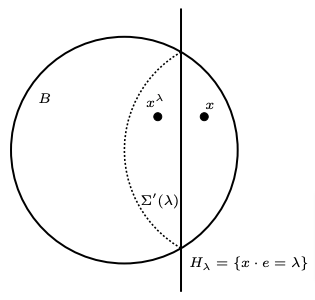
Figure 2. The reflected cap.

and the reflection $u^\lambda$ of $u$ with respect to the critical hyperplane lies below $u$ in the reflected cap (see Figure 3).

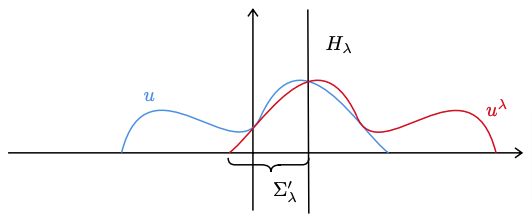
The function $u$ and its reflected with respect to $H_\lambda$

At this point, by means of the maximum principle, one can prove the symmetry properties of the function $u$ .

In the spirit of generalizing the result by Gidas, Ni, and Nirenberg, we wonder if the symmetry still holds when different boundary conditions on $\partial B$ are prescribed. We focus on the following problem

$\begin{cases} -\Delta u= f(u) & \text{in } B,\\ \displaystyle{\frac{\partial u}{\partial \nu}+ \beta u=0} & \text{on } \partial B, \end{cases} (3)$

where $\beta$ is a positive parameter and $\nu$ is the unit exterior normal to $\partial B$ . These are the so-called Robin boundary conditions. Is it true that the symmetry holds under suitable assumptions on $f$ and $u$ ?
Unfortunately, it seems that the moving plane method cannot be applied when dealing with Robin boundary conditions, because of the lack of a suitable maximum principle.

Moreover, we found out that it is always possible to build a function $\varphi: B\to \R$

$\varphi(x)=\frac{1}{(|x-x_0|^2+1 -|x_0|^2)^\beta}, \quad x_0\in B,$

such that
• $\varphi$ is non-radial, $\varphi(x)\neq\varphi(|x|)$ ;
• $\varphi\in C^{\infty}(\overline{B})$ ;
• $\varphi$ is positive;
• $\varphi$ is a solution to (3), with right hand side $f$

$f(t)=2\beta t\left[(n-2(\beta+1)) t^\frac{1}{\beta}+ 2(\beta+1)(1-|x_0|^2) t^\frac{2}{\beta}\right]$

that is a Lipschitz function. Moreover, by imposing some bounds on $\beta$ , the function $f$ is positive.

So, the symmetry result cannot hold in the case of Robin boundary conditions.

This result is contained in [2].

References

[1] A. D. Aleksandrov. Uniqueness theorems for surfaces in the large. V. Amer. Math. Soc. Transl. (2), 21:412–416, 1962.
[2] A. Celentano, A. L. Masiello, and G. Paoli. A counterexample to the classical Gidas Ni and Nirenberg symmetry result in the case of Robin boundary conditions. https://arxiv.org/abs/2304.00806, 2023.
[3] B. Gidas, W.-M. Ni, and L. Nirenberg. Symmetry and related properties via the maximum principle. Comm. Math. Phys., 68(3):209–243, 1979.
[4] J. Serrin. A symmetry problem in potential theory. Arch. Rational Mech. Anal., 43:304–318, 1971.