The ADMM-PINNs Algorithmic Framework for Nonsmooth PDE-Constrained Optimization: A Deep Learning Approach
Motivation
This post shows the source code from the paper “The ADMM-PINNs Algorithmic Framework for Nonsmooth PDE-Constrained Optimization: A Deep Learning Approach”. (See reference below)
We study the combination of the alternating direction method of multipliers (ADMM) with physics-informed neural networks (PINNs) for a general class of nonsmooth partial differential equation (PDE)-constrained optimization problems, where additional regularization can be employed for constraints on the control or design variables. The resulting ADMM-PINNs algorithmic framework substantially enlarges the applicable range of PINNs to nonsmooth cases of PDE-constrained optimization problems. The application of the ADMM makes it possible to untie the PDE constraints and the nonsmooth regularization terms for iterations. Accordingly, at each iteration, one of the resulting subproblems is a smooth PDE-constrained optimization which can be efficiently solved by PINNs, and the other is a simple nonsmooth optimization problem which usually has a closed-form solution or can be efficiently solved by various standard optimization algorithms or pre-trained neural networks. The ADMM-PINNs algorithmic framework does not require to solve PDEs repeatedly, and it is mesh-free, easy to implement, and scalable to different PDE settings. We validate the efficiency of the ADMM-PINNs algorithmic framework by different prototype applications, including inverse potential problems, source identification in elliptic equations, control constrained optimal control of the Burgers equation, and sparse optimal control of parabolic equations.
GitHub Repository
Download resources from our FAU DCN-AvH GitHub, at: https://github.com/DCN-FAU-AvH/ADMM-PINNs
Requirements
To run the code, you will need the following packages:
1. Jupyter Notebook
2. PyTorch
3. NumPy
4. SciPy
5. Plotly
6. Matplotlib
7. CUDA (Optional)
We recommend using Conda to manage your packages.
Demo
Each .ipynb file in this repository can be executed in a Jupyter Notebook, and its name corresponds to its functionality.
There are also several .py files in the repository that serve as the foundation for implementing 2-dimensional finite element methods.
Additionally, there are modelxx_norm.pth files that contain pre-trained denoisers of CNNs:
• These files can be generated using generate_denoiser.ipynb, but you will need to download the BSD68 training set yourself.
• generate_denoiser.ipynb is the PyTorch version of the original code.
Cases
The four cases included are:
Inverse_Potential
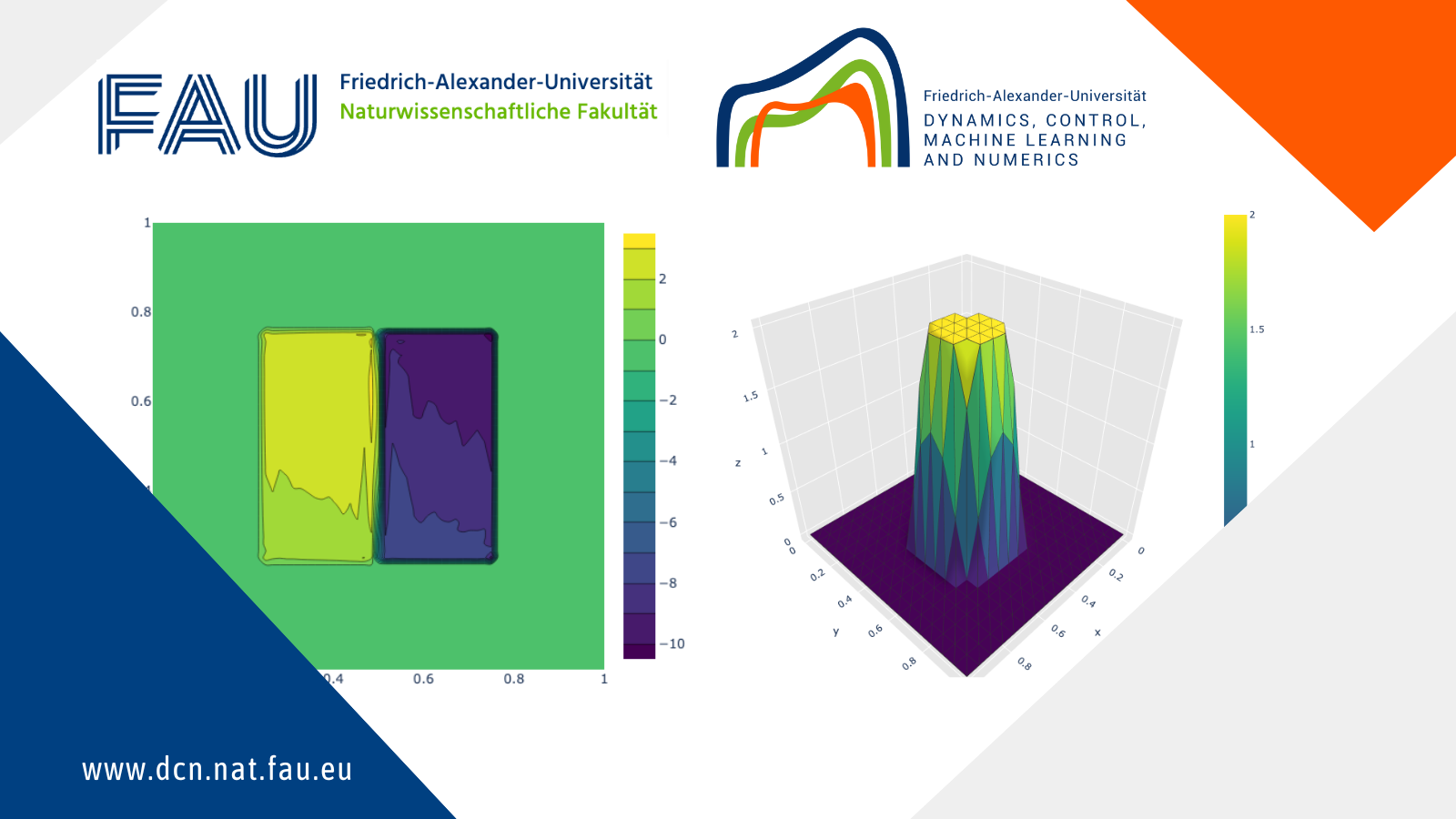
The source code for solving the Inverse Potential Problem.
Burgers
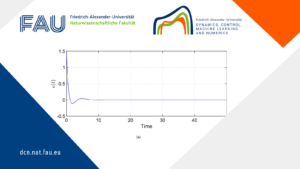
The source code for solving the Control Constrained Optimal Control of the Burgers Equation.
SourceID
The source code for Discontinuous Source Identification for Elliptic PDEs.
L1Control
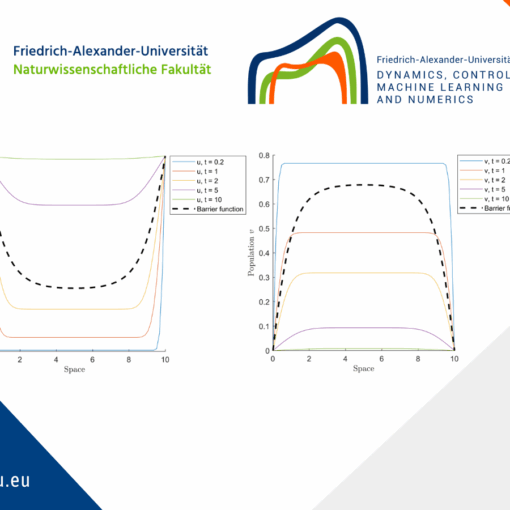
The source code for solving Sparse Optimal Control of Parabolic Equations.
Numerical results
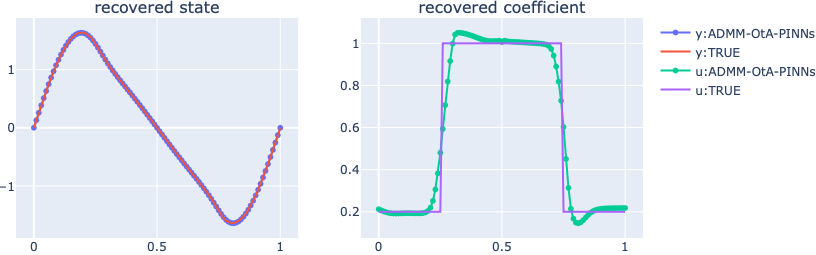
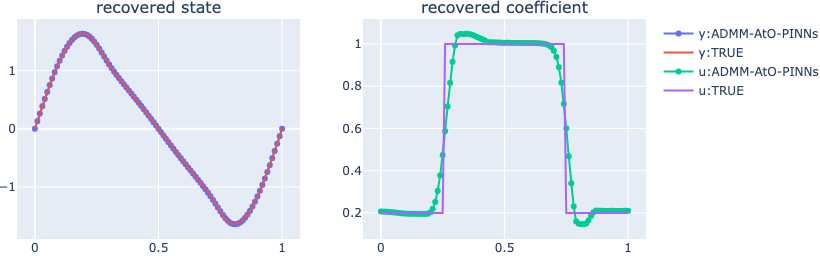
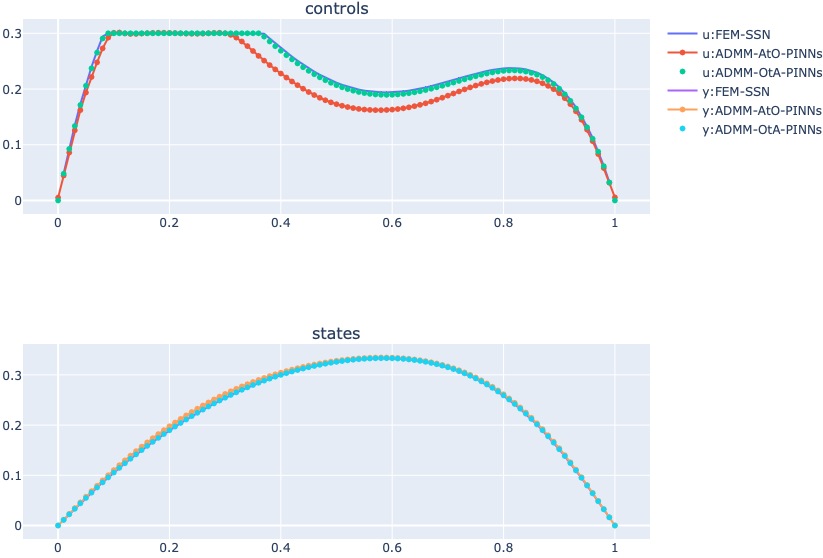
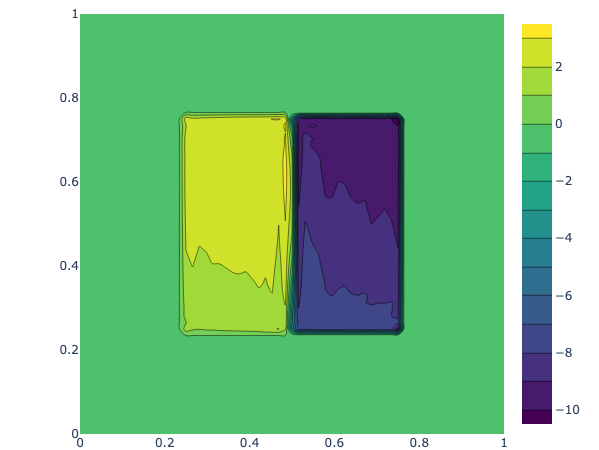
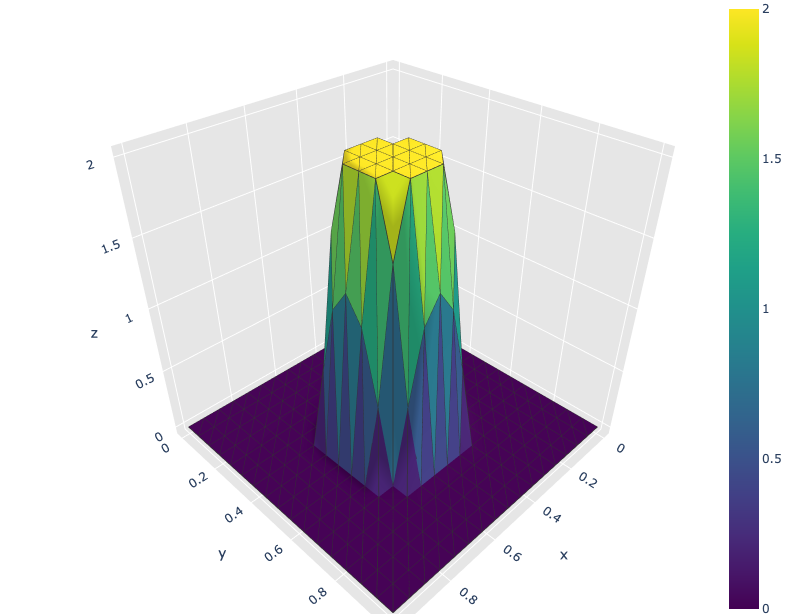
References
Yongcun Song, Xiaoming Yuan, Hangrui Yue. The ADMM-PINNs Algorithmic Framework for Nonsmooth PDE-Constrained Optimization: A Deep Learning Approach. https://doi.org/10.48550/arXiv.2302.08309