Master PDE course – Partial Differential Equations, Control and Numerics

02 Finite-dimensional linear control
Finite-dimensional linear control

03 Basic Tools
- Gradient descent Methods
- An Algorithm for Density
- Background on Fourier Analysis
- Ingham’s inequality
- Adjoint Methods

04 Waves
- Waves, history and applications
- Finite difference schemes and numerical dispersion
- 1d-Waves: Propagation, Control & Numerics
- Waves in non smooth media
- Wave propagation and discontinuous Garlerkin approximations
- Observability of time-discrete conservative systems
- Control of semilinear waves
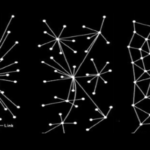
05 Waves on Networks

06 Heat Processes

07 Heat Waves
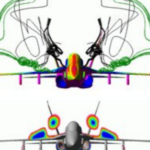
08 Hybrid systems of PDE
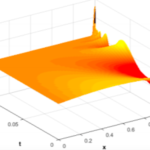
09 Parameter depedence
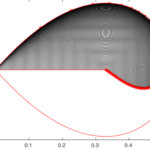
10 Control of some diffusive models
Reaction-diffusion models: dynamics, control and numerics
11 Turnpike and Constraints
12 Time InversionInverse time designInverse design of one-dimensional Burgers equationFlow control in the presence of shocks
Inverse-time design for Hamilton-Jacobi equations
13 Viscous Hamilton-Jacobi
Control of viscous Hamilton-Jacobi equations

14 NonLocal
Control of PDEs involving non-local terms

15 Hardy
Hardy inequalities, heat kernels and wave propagation
16 Age structured
Control of a Population Dynamics Model with Age Structuring and Diffusion

17 Kolmogorov equation

18 Guidance
Dynamics and control for multi-agent networked systems
Model Predictive Control with Random Batch Methods for a Guiding Problem
19 Optimal Location sensors

20 Decay Partially Dissipative Hyperbolic
21 Dispersive Numerics

22 Homogenization, numerics and design

23 Data Sciences
24 Free boundaries
25 DyCon Toolbox

26 Data-Driven COVID Modeling
27 Open problems






