Sentiment Analysis with Transformers This post includes an app SentimentAnalysisTransformersApp created for a public outreach activity organized by the Chair for Dynamics, Control, Machine Learning and Numerics – Alexander von Humboldt Professorship (FAU DCN-AvH) during the Lange Nacht der Wissenschaften 2025 (Long Night Sciences 2025). Live demo https://albertalcalde.github.io/SentimentAnalysisTransformersApp/ Overview This […]
Hub
18 posts
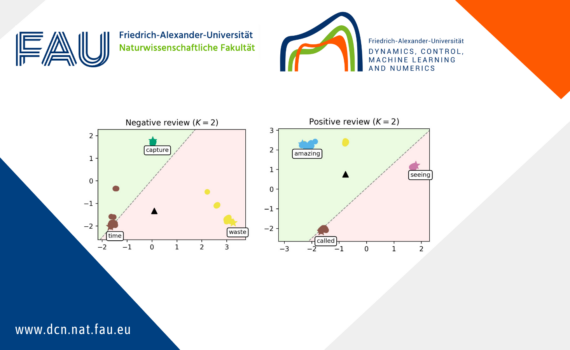
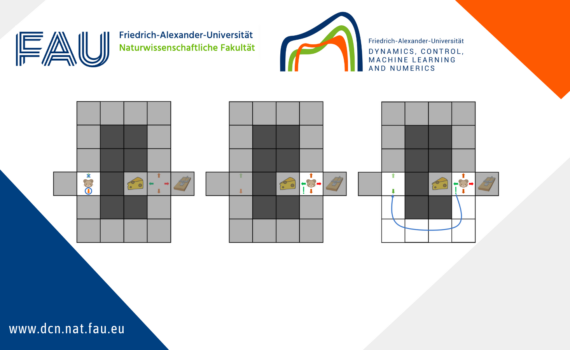
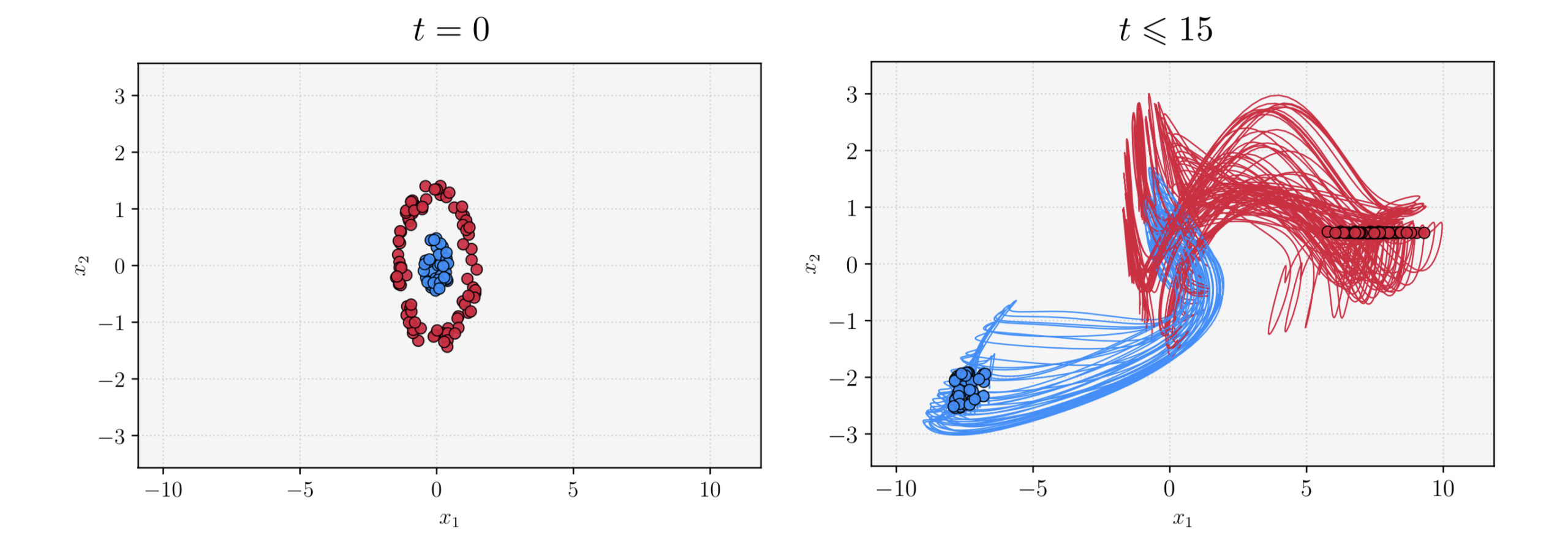
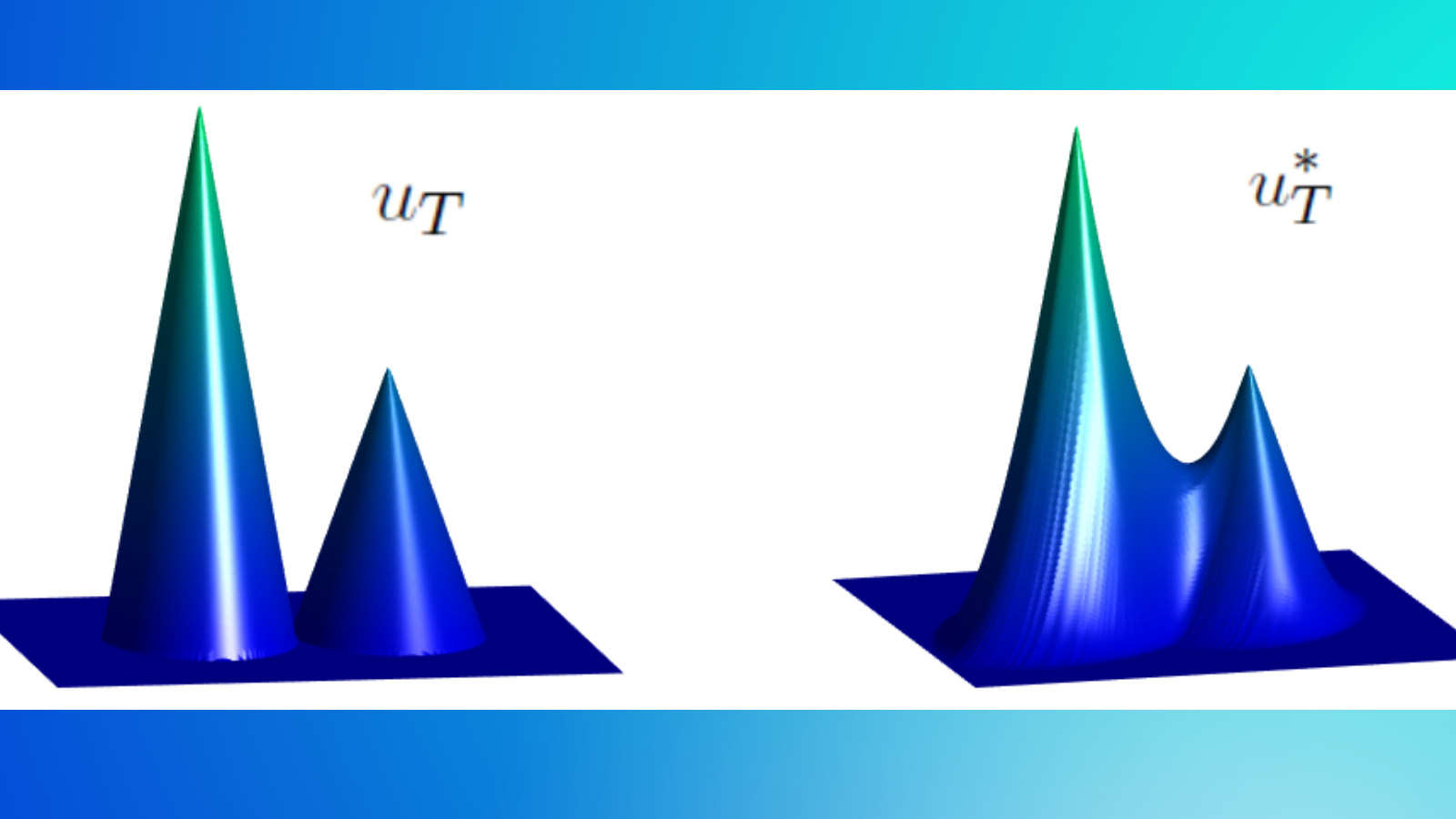
Clustering in pure-attention hardmax transformers and its role in sentiment analysis This post provides an overview of the results in the paper Clustering in Pure-Attention Hardmax Transformers and its Role in Sentiment Analysis by Albert Alcalde, Giovanni Fantuzzi, and Enrique Zuazua [1]. Codes used to reproduce the simulations can be […]
PINNs Introductory Code for the Heat Equation This repository provides some basic insights on Physics Informed Neural Networks (PINNs) and their implementation. PINNs are numerical methods based on the universal approximation capacity of neural networks, aiming to approximate solutions of partial differential equations. Recently, extensive focus has been on approximating […]
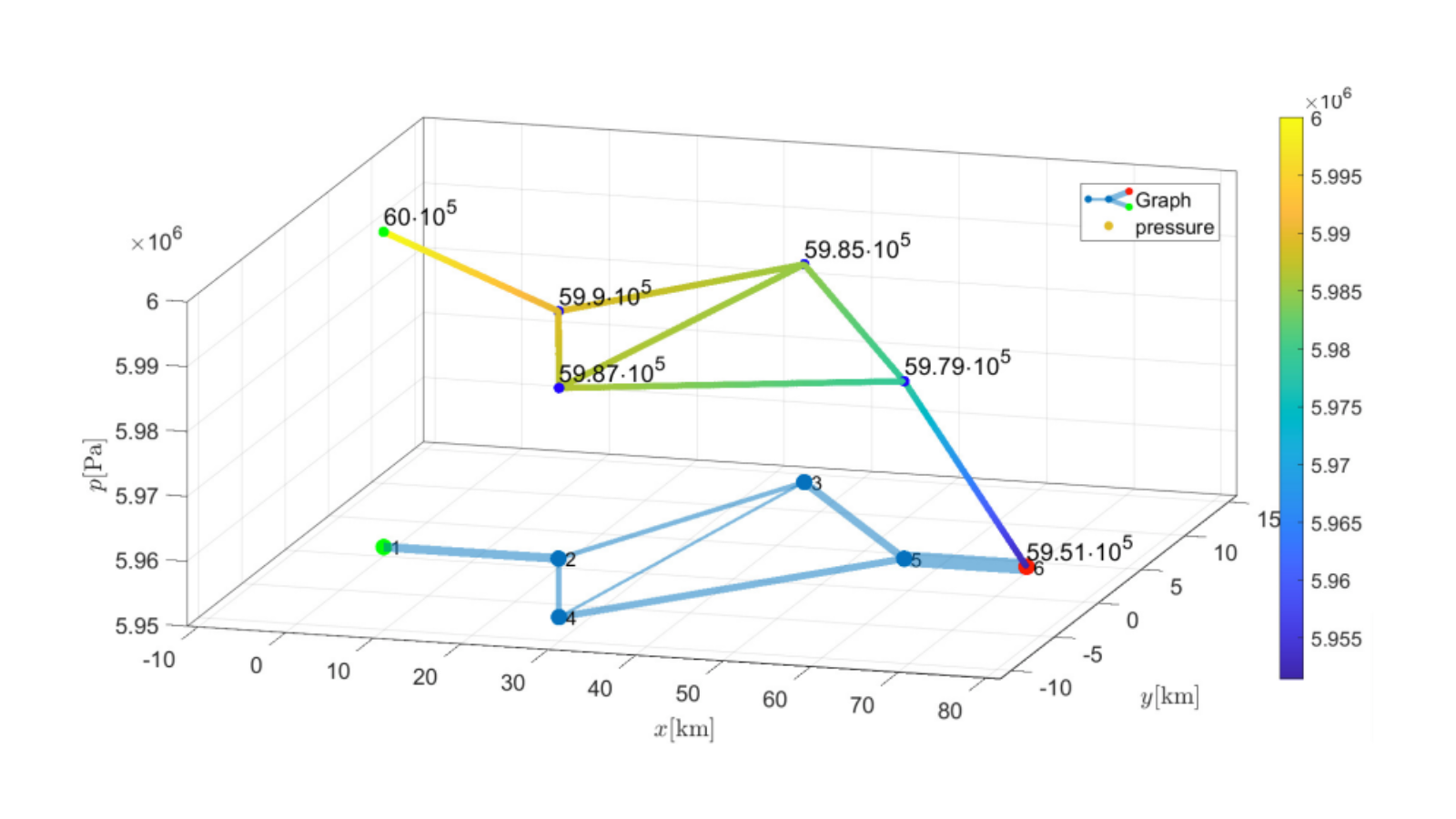
Combined convection and diffusion in a network. A numerical analysis. The problem: a contaminant in a network of water pipes Imagine that there is a network of pipes full of water. The water is flowing from some source nodes (say, some water plants) to some destination nodes (say, people’s homes). […]
The ADMM-PINNs Algorithmic Framework for Nonsmooth PDE-Constrained Optimization: A Deep Learning Approach Motivation This post shows the source code from the paper “The ADMM-PINNs Algorithmic Framework for Nonsmooth PDE-Constrained Optimization: A Deep Learning Approach”. (See reference below) We study the combination of the alternating direction method of multipliers (ADMM) with […]
Reinforcement learning as a new perspective into controlling physical systems Introduction Optimal control addresses the problem of bringing a system from an initial state to a target state, like a satellite that we want to send into orbit using the least possible amount of fuel. Since the last century, mathematics […]
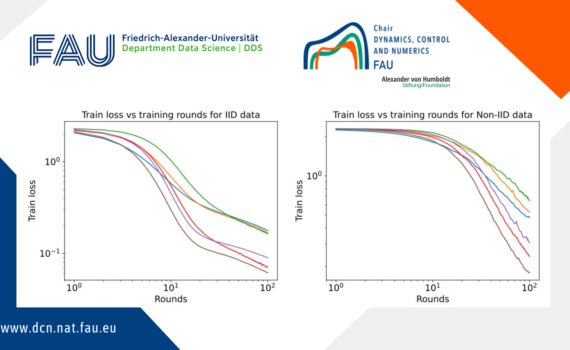
Federated Learning: Protect your data and privacy Code: A basic PyTorch implementation of the FedAvg algorithm (GitHub) Federated Learning is becoming an increasingly popular topic in machine learning. But what is it, and why do we need it? To explain what the excitement is all about, this post outlines the […]
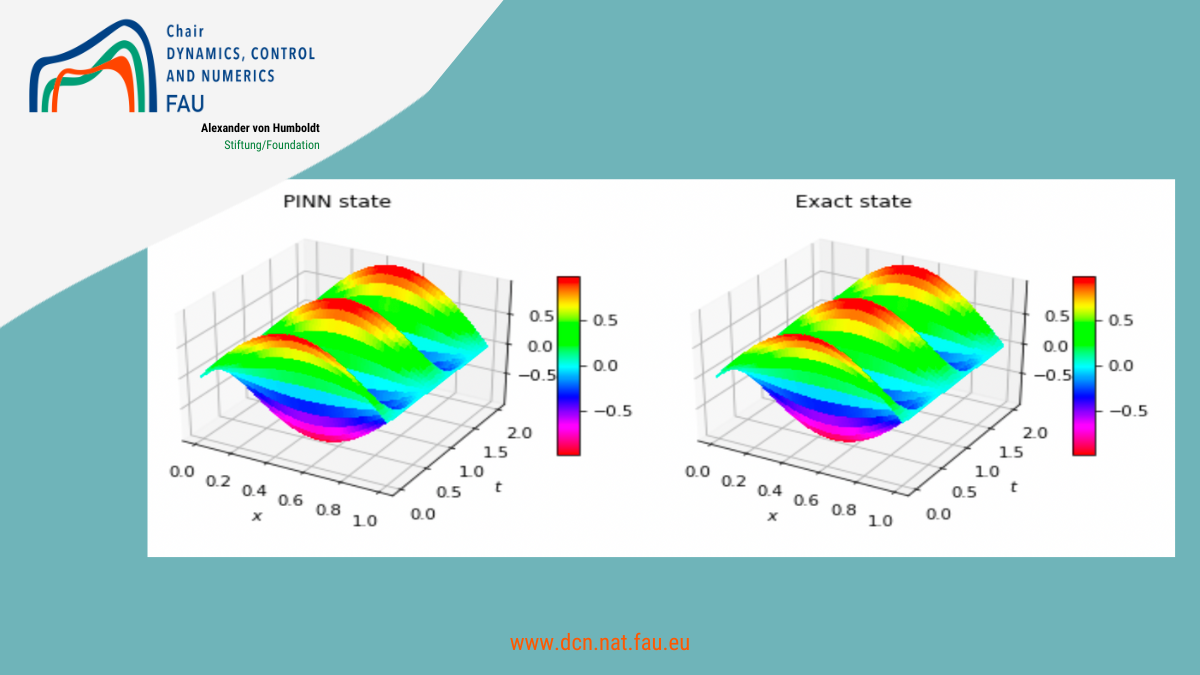
Approximating the 1D wave equation using Physics Informed Neural Networks (PINNs) Introduction Accurate and fast predictions of numerical solutions are of significant interest in many areas of science and industry. On one hand, most theoretical methods used in the industry are the result of deriving differential equations that are […]
Start with tutorials to get familiar with the code Tutorial 1: Train a neural ODE based network on point cloud data set and generating a gif of the resulting time evolution of the neural ODE Code: Code is based on GitHub: borjanG : 2021-dynamical-systems that uses the torchdiffeq package GitHub […]
Gas networks at stationary states: Analysis, software and visualization Code: Files to run: nocircle.m, onecircle.m or twocircles.m 1 Introduction This post presents the results of my Bachelor thesis about the modeling and implementation of gas networks at stationary states. Using the isothermal Euler equations to describe the gas flow […]
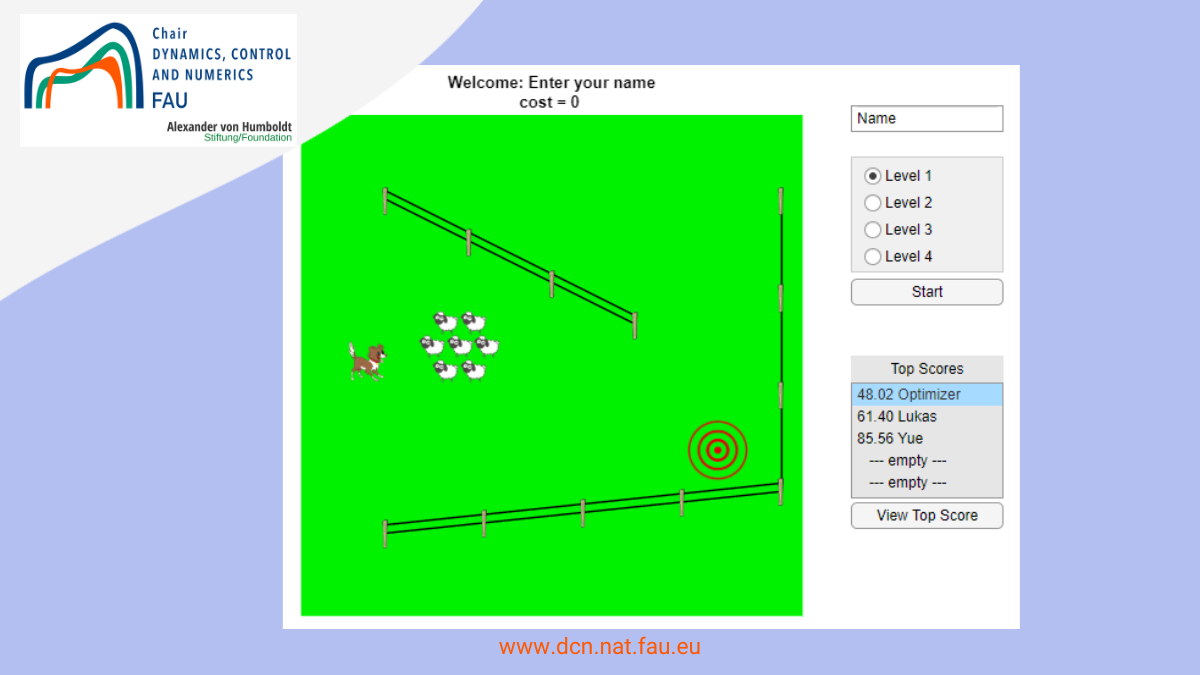
Author: Daniël Veldman, FAU DCN-AvH Code: A sheep herding game in MATLAB developed for the Long Night of Science #NdW22 (Lange Nacht der Wissenschaft) Erlangen-Furth-Nuernberg 2022. Main rules • The dog should drive sheep to the target (red). • You can steer the dog with the arrow keys. • The […]
Author: Martín Hernández, FAU DCN-AvH Code: In this repository, we show a code for Lloyd’s algorithm. Also called Voronoid iteration, this is an iterative algorithm finding for equispaced convex cells in euclidean space. Lloyd’s algorithm finds the distribution of the cells computing their center of mass and iteratively applying the […]
The code implements the gradient regularization method of robust training in the setting of neural ODEs. Various jupyter notebooks are included that generate plots comparing standard to robust training for 2d point clouds. Code: A good starting point is robustness_plots.ipynb Code is based on GitHub: borjanG : 2021-dynamical-systems that uses […]
Author: Borjan Geshkovski, MIT The interplay of control and Deep Learning By Borjan Geshkovski It is superfluous to state the impact deep (machine) learning has had on modern technology, as it powers many tools of modern society, ranging from web searches to content filtering on social networks. It is […]
Author: Martin Gugat, Enrique Zuazua, Aleksey Sikstel, FAU DCN-AvH Code: [HINT] To run the software on your computer, you may have to install additional standard software packages (like cmake and a c++ compiler) and additional libraries (lapack, PETSc). In order to optimize the operation of gas transportation networks, […]
Author: Carlos Esteve, Deusto CCM Code: In a previous post “Inverse Design For Hamilton-Jacobi Equations“, described all the possible initial states that agree with the given observation of the system at time on the reconstruction of the initial state in many evolution models. Our goal here is to study the […]
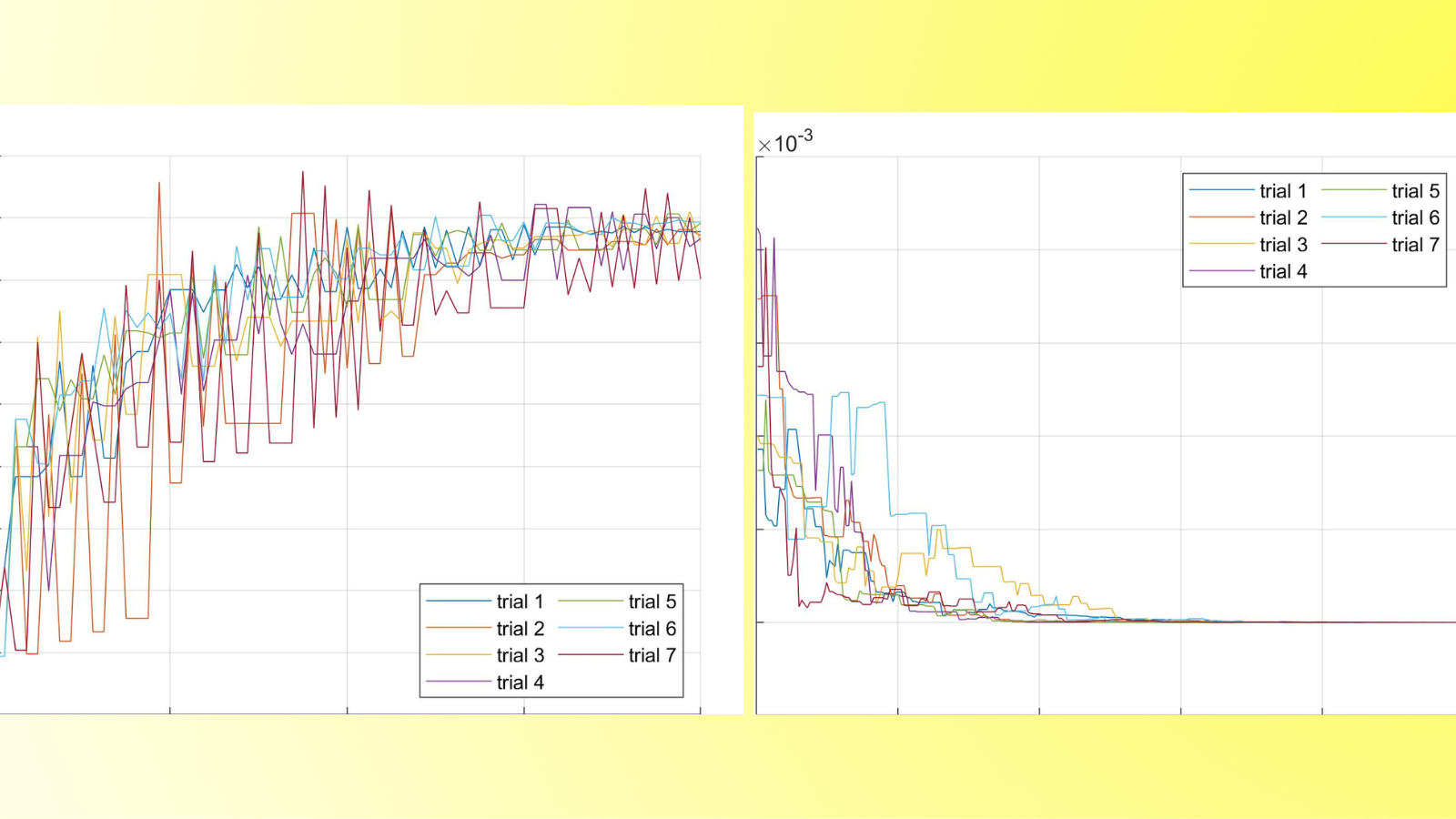
Author: Daniel Veldman, FAU DCN-AvH Code: || Also available @Daniël’s GitHub In a previous post “Randomized time-splitting in linear-quadratic optimal control“, it was proposed to use the Random Batch Method (RBM) to solve classical Linear-Quadratic (LQ) optimal control problems. This contribution is concerned with the corresponding numerical implementation. We thus […]
Author: Alexei Gazca, FAU DCN-AvH Code: Below is a description of the types of problems that can be tackled using the code contained in this repository. Solving linear systems arising from the discretisation of partial differential equations can be an extremely challenging and computationally intensive task, especially for problems […]