Date: Mon. June 5, 2023 at 11:00H Organized by: FAU DCN-AvH, Chair for Dynamics, Control, Machine Learning and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: Learning of Dynamic Processes Speaker: Prof. Dr. Juan-Pablo Ortega Affiliation: Nanyang Technological University (Singapore) Abstract. The last decade has seen […]
darlis.dcn
The FAU DCN-AvH, Chair for Dynamics, Control, Machine Learning and Numerics at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) is looking for several PhD and PostDocs on the topics: -Machine Learning and Control Theory -Long-time asymptotics of partial differential equations (PDE) -Numerical analysis of PDE -Control and Optimal Design -PDEs in networks Join […]
Math Crash Course FAU DCN-AvH. Friedrich-Alexander Universität Erlangen-Nürnberg (Germany) Period: 2023 _ The math final exams are coming up and you’re still unsure? Don’t worry, with our Math Abi Crash Course, we can support you in mastering the Math Abi! In this course, we will work together on past year’s […]
Next May 31, 2023 our Head Prof. Enrique Zuazua will talk on “Control, Cibernética e Inteligencia Artificial” at the Coloquio Virtual Latinoamericano: Control, Cibernética e Inteligencia Artificial organized by CRC, Computational Science Research at San Diego State University (USA). Abstract. El control de sistemas, o la cibernética, según el término […]
Date: Tue. May 30, 2023 Event: FAU MoD Lecture Organized by: FAU MoD, Research Center for Mathematics of Data at Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) FAU MoD Lecture: From Physics-Informed Machine Learning to Physics-Informed Machine Intelligence: Quo Vadimus? Speaker: Prof. Dr. George Em Karniadakis (GS h-index 129) The Charles Pitts Robinson and […]
Date: Fri. May 26, 2023: Event: FAU DCN-AvH Mini-workshop: Analysis, Numerics and Control Organized by: FAU DCN-AvH, Chair for Dynamics, Control, Machine Learning and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) 14:00H Title: Convex functions and its applications Speaker: Prof. Dr. Çetin Yildiz Affiliation: Visiting Scientist […]
On May 22, 2023 our Head Prof. Enrique Zuazua will talk on “Controllability of Neural Differential Equations” at the 4th AFOSR Monterey Training Workshop on Computational Issues in Nonlinear Control-Topics organized on May 22-24, 2023 in California thanks to Air Force Office of Scientific Research (AFOSR) and University of California, […]
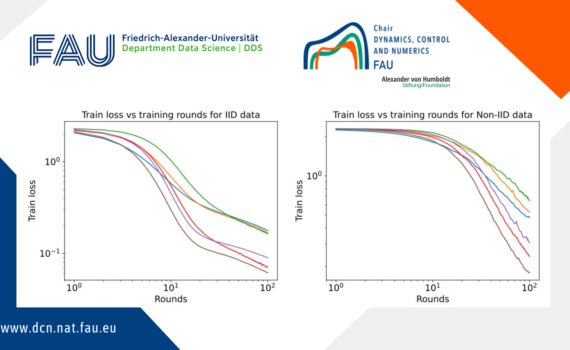
Master Thesis: “Gradient Descent on Wide Neural Networks and Federated Learning” Author: Gisele Stephanie Otiobo Supervisor: Prof. Dr. DhC. Enrique Zuazua Date: May 20, 2023 Deep neural networks are very complex and difficult to understand due to their intricate structure and a vast number of parameters. The relationship between parameters […]
Next Wed. May 17, 2023 at 19:00H our Head Prof. Enrique Zuazua will talk on “Numerics, Dynamics, Control and Machine Learning” at the Seminario de EDP e Matematica Aplicada organized by UFF, UFRJ, LNCC, U. Sevilla, UdeC and UEM (Brazil, Portugal, Spain, Peru, Chile). Abstract. In this lecture we shall […]
Inria International Chairs holder In May 2023, Prof. Enrique Zuazua has been awarded as a Holder of Inria International Chair to set up/reinforce an existing collaboration with the Inria teams. Topic: Control and Scientific Machine Learning Years: 2023-2027 • Check the the holders (2023) of Inria International Chairs. _ Don’t […]
Date: Thursday, May 11, 2023: Event: FAU DCN-AvH mini-workshop: Analysis, Numerics and Control Organized by: FAU DCN-AvH, Chair for Dynamics, Control, Machine Learning and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) 14:00H Title: Optimal control for suppression of singularity in chemotaxis Speaker: Prof. Dr. Weiwei Hu […]
Next May 11, 2023 at 10:10H our Head Prof. Enrique Zuazua will talk on “Control and Machine Learning” at the conference Optimization and Control in Burgundy that aims to gather mathematicians from the two fields Optimization and Control to promote new exchanges and collaborations organized from May 9th-11st, 2023 at […]
On Tuesday May 9, 2023 our postdoctoral researcher Michael Schuster, will talk on “Nodal Control and Probabilistic Constrained Optimization using the Example of Gas Networks” at Kolloqium Mathematik organized by the Department Mathematik at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany). Abstract. Uncertainty often plays an important role in gas transport and probabilistic […]
Breaking the symmetry with Robin boundary conditions Introduction Establishing symmetry properties of solutions to differential equations is a very important task in mathematical analysis, both from the theoretical point of view and for applications. Indeed, partial differential equations arise in modeling many phenomena in physics, mechanics, and so on. A […]
Date: Wed. May 03, 2023: Event: FAU DCN-AvH Seminar Organized by: FAU DCN-AvH, Chair for Dynamics, Control, Machine Learning and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: Inviscid limits of the compressible Navier-stokes equation to small BV solutions to Euler Speaker: Prof. Dr. Alexis Vasseur […]
Date: Thu. April 27, 2023 Time: 09:45H (11:45H GST) Where? On-site On April 27, 2023 our Head Prof. Enrique Zuazua will talk as keynote speaker on “Control and Machine Learning” at the ICMSAO’23, a venue for engineers and scientists from all over the world to share their latest research results […]
On Wednesday April 26, 2023, Prof. Dr. Joachim Hornegger, President of FAU and Prof. Dr. Veronica Grimm, member at FAU MoD will open the #FAUinsights lectures organised by FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg and EnCN, Energie Campus Nürnberg to discuss on hydrogen and its possible applications: • FAU’s hydrogen strategy (“Die Wasserstoffstrategie der FAU”) By […]
Date: Thu. April 20, 2023 at 11:00H Event: FAU DCN-AvH Seminar Organized by: FAU DCN-AvH, Chair for Dynamics, Control, Machine Learning and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: Error bounds for physics-informed (and) operator learning for PDEs Speaker: Tim De Ryck Affiliation: PhD Student […]
Date: Wed. April 19, 2023 Event: FAU MoD Lecture Organized by: FAU MoD, Research Center for Mathematics of Data at Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: From Alan Turing to contact geometry: Towards a “Fluid computer” Speaker: Prof. Dr. Eva Miranda Affiliation: UPC, Universitat Politècnica de Catalunya · BarcelonaTech Abstract. Is hydrodynamics […]
Date: Mon. April 17, 2023 Time: 16:00H Where? On-site / Online (zoom link below) On April 17, 2023 our Head Prof. Enrique Zuazua will talk on “Control and Machine Learning” at the Workshop Geometric Aspects of Evolution and Control organized on April 17-21, 2023 at the FernUniversität Hagen, Germany. Abstract. […]
CML: Control, Machine Learning and Numerics Professors: Enrique Zuazua, Yongcun Song Period: Summer Semester 2022/2023 Date: April to July 2023 ECTS: 10 This course at FAU StudON: https://www.studon.fau.de/studon/goto.php?target=crs_5073175
Course: Wave Phenomena Lecturers: Enrique Zuazua, Nicola De Nitti Period: 2022/2023 summer semester Date: April – July 2023 Location: FAU. Master’s Degree in Computational and Applied Mathematics ECTS: 10 This course at FAU StudON: –
Course: Scalar Conservation Laws Lecturers: Enrique Zuazua, , Nicola De Nitti Period: 2022/2023 summer semester Date: April – July 2023 Location: FAU. Master’s Degree in Computational and Applied Mathematics ECTS: 10 This course at FAU StudON: –
Control of multi-particle systems, mean-field limits, and applications to deep learning (Steuerung von Mehrteilchensystemen, Mean-Field Limits und Anwendungen für Deep Learning) Project Nº: 530756074 Affiliated Entities: Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU, Germany), Catholic University of Korea (CUK, South Korea) Supported by DFG (Deutsche Forschungsgemeinschaft/ German Research Foundation) and NRF. Südkorea-NRF-DFG-2023 programme Duration: […]
Convolutional autoencoders for very low-dimensional parametrizations of nonlinear fluid flow 1. Introduction The control of large-dimensional nonlinear dynamical systems is a challenging task because of the 1. system’s size that means a high demand in computational resources 2. and the nonlinearity that adds model inherent complexity to be resolved by […]
Millions in funding for Humboldt Professor Enrique Zuazua Another FAU researcher has prevailed in the competitive process for the Advanced Grants of the European Research Council (ERC): The mathematician and Humboldt Professor Dr. Enrique Zuazua will receive up to 2.5 million euros for his project “Control for Deep and Federated […]
Date: Wed. March 29, 2023: Event: FAU DCN-AvH Seminar Organized by: FAU DCN-AvH, Chair for Dynamics, Control, Machine Learning and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: Event-Triggered Control Using a Positive Systems Approach Speaker: Prof. Dr. Michael Malisoff Affiliation: LSU, Louisiana State University (USA) […]
Date: Mon. March 27, 2023: Event: FAU DCN-AvH Mini-workshop: Analysis, Numerics and Control Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) 11:00H Title: Null Controllability for Population Dynamics with age, size Structuring and Diffusion Speaker: Prof. Dr. Yacouba […]
Date: Thursday March 16, 2023 Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: Shape optimization problems in thermal insulation with thin insulating layers Speaker: Paolo Acampora Affiliation: PhD Student from Università degli Studi di Napoli Federico II […]
Date: Wednesday March 15, 2023 Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: Parabolic trajectories and the Harnack inequality Speaker: Lukas Niebel Affiliation: Ulm University Abstract. In this talk, we will study the Harnack inequality for weak […]
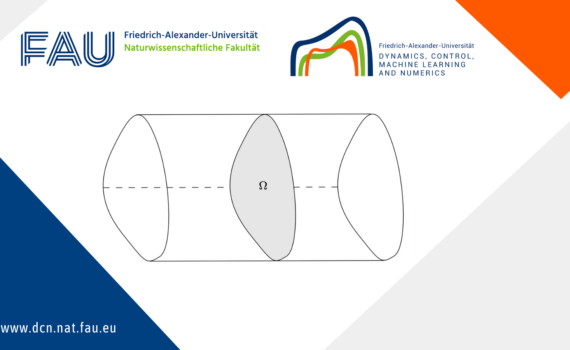
Torsional Rigidity: Classical and new results Torsional rigidity is a key quantity to characterize how a beam responds to applied forces. The higher the torsional rigidity, the harder it is to deform the beam. A natural question arises: which shape for the beam’s cross section yields the highest torsional rigidity? […]
Next Wednesday March 15, 2023 our Prof. Akad. Director Martin Gugat, will talk on “Observer Systeme für Gasnetze” at the ,Elgersburg Workshop’ at TU Ilmenau, Technische Universität Ilmenau on March 12-16th, 2023. Abstract. Pipeline networks correspond to graphs where the edges are given by the pipes that form the network. […]
Date: Thursday March 9, 2023 Event: FAU DCN-AvH Seminar Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: A Deep Learning approach to Reduced Order Modeling of Parameter dependent Partial Differential Equations Speaker: Prof. Dr. Paolo Zunino Affiliation: […]
Date: Thursday March 2, 2023 Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) FAU DCN-AvH Seminar “Conservation laws on a star-shaped network” Speaker: Prof. Dr. Carlotta Donadello Affiliation: Université de Franche-Comté (France) Abstract. Hyperbolic conservation laws defined on […]
BAYLAT and the chair “Dynamics, Control and Numerics – Alexander von Humboldt Professorship” of FAU sign an agreement to promote the exchange of talents in mathematical research On February 27, 2023, BAYLAT and the Chair “Dynamics, Control and Numerics – Alexander von Humboldt Professorship” (DCN-AvH) at Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) officially […]
On Monday March 6, 2023 our Head Prof. Enrique Zuazua will talk on “Control and Machine Learning” organized by the Mechanical and Aerospace Engineering at UC San Diego (USA). Abstract. In this lecture we shall present some recent results on the interplay between control and Machine Learning, and more precisely, […]
Date: Tuesday February 14, 2023 Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: Towards a better description of sea states Speaker: Dr. Susanne Støle-Hentschel Affiliation: École Normale Supérieure Paris-Saclay (France) Abstract. In the light of climate change, […]
Date: Tuesday February 14, 2023: Event: FAU DCN-AvH Mini-workshop: Variational Methods, Functional Inequalities, and Shape Optimization Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) 15:00H Title: Fractional Pohozaev Identities Speaker: Dr. Sidy Moctar Djitte Affiliation: Postdoctoral researcher at […]
Date: Thursday February 9, 2023 Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: Towards a better description of sea states Speaker: Dr. Guy Foghem Affiliation: Technische Universität Dresden (Germany) Abstract. Within the framework of Hilbert spaces, we […]
Date: Wed. February 1, 2023 Event: FAU MoD Lecture Organized by: FAU MoD, Research Center for Mathematics of Data at Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Speaker: Prof. Dr. Nick Trefethen Affiliation: University of Oxford This FAU MoD Lecture will have two sessions: [Session 1] Main lecture (10:30H – 11:30H) (On-site / online) […]
Date: Friday, January 20, 2023: Event: FAU DCN-AvH Seminar Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU, Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: FAU DCN-AvH Seminar “Consensus-based High Dimensional Global Non-convex Optimization in Machine Learning” Speaker: Prof. Dr. Shi Jin Affiliation: Shanghai Jiao […]
Date: Wed. January 18, 2023 Event: FAU DCN-AvH Seminar Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: FAU DCN-AvH Seminar “Lagrangian controllability of the incompressible Navier-Stokes equations” Speaker: Prof. Dr. Franck Sueur Affiliation: Institute of Mathematics of […]
Control, inversion and numerics for Partial Differential Equations (CIN-PDE) Project Nº: M-0548 Affiliated Entities: Fudan University (FDU, Shanghai), Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU, Germany) Supported by Sino-German Mobility Programme from Chinesisch-Deutsches Zentrum für Wissenschaftsförderung located in NSFC (National Natural Science Foundation of China) and DFG (Deutsche Forschungsgemeinschaft/ German Research Foundation) Duration: 2022 […]
Federated Learning: Protect your data and privacy Code: A basic PyTorch implementation of the FedAvg algorithm (GitHub) Federated Learning is becoming an increasingly popular topic in machine learning. But what is it, and why do we need it? To explain what the excitement is all about, this post outlines the […]
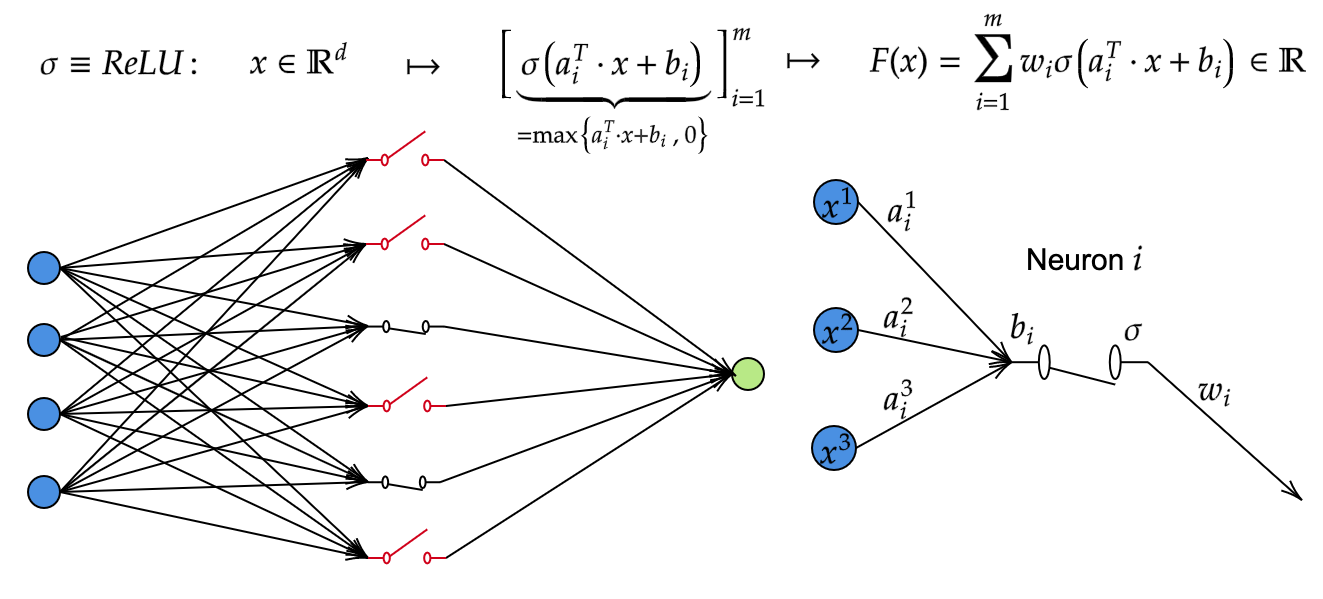
Breaking the curse of dimensionality with Barron spaces 1 Introduction Recent advances in computational hardware have enabled the implementation of the set of algorithmic methods known as Deep Learning, whose development nevertheless dates back several decades. In this way, they have emerged in the latest years as the main tool […]
DTN MoDConFlex. Modelling and control of flexible structures interacting with fluids Project/grant No.: 101073558 Affiliated Entities: Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Bergische Universität Wuppertal, Tel Aviv University, Universiteit Twente, Université Bourgogne Franche-comté (UBFC), Université de Bordeaux Supported by HORIZON TMA MSCA. Marie Skłodowska-Curie Doctoral-Training-Network Duration: 2023 – 2027 The network brings together 17 […]
Date: Wed. December 07, 2022: Event: FAU DCN-AvH Seminar Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: FAU DCN-AvH Seminar “Gaussian random interface models and discrete Green’s functions” Speaker: Dr. Florian Schweiger Affiliation: Weizmann Institute of Science […]
Stability results for the KdV equation with time-varying delay Introduction The Korteweg-de Vries equation (KdV), is a third-order nonlinear one-dimensional equation given by . It was introduced in [6] to model the propagation of long water waves in a channel. In the last few years, the controllability and stabilization properties […]
Date: Wed. November 30, 2022 Event: FAU DCN-AvH Seminar Organized by: FAU DCN-AvH, Chair for Dynamics, Control and Numerics – Alexander von Humboldt Professorship at FAU Friedrich-Alexander-Universität Erlangen-Nürnberg (Germany) Title: FAU DCN-AvH Seminar “Compensated Integrability and Conservation Laws” Speaker: Prof. Dr. Denis Serre Affiliation: Ecole Normale Supérieure de Lyon (France). […]
BaCaTeC. Control and Machine Learning Enrique Zuazua, Miroslav Krstic Supported by HighTech Research between Bavaria and California (BaCaTeC, Bayerisch-Kalifornische Hochschulzentrum) Duration: 2023 – 2025 Machine Learning (ML) is forging a new era in Applied Mathematics (AM), generating rich, intensive, innovative research, insightful new ideas and powerful methods. However, simultaneously, this is […]