Nonlinear hyperbolic systems: Modeling, controllabiliy and applications The control theory of hyperbolic systems is an important topic in continuum and fluid mechanics. Networks of nonlinear hyperbolic systems arise in real world applications, e.g. planar or out-of-plane networks of vibrating strings, shearable beams, gas networks and shallow water systems. On these […]
Math
82 posts
Kinetic theory of Bose Einstein Condensates If a dilute gas of bosons, about one-hundred-thousandth the density of normal air, is cooled to a temperature very close to absolute zero (0 K or -273.15C), the gas will be changed into a new state of matter, called Bose-Einstein condensate (BEC). This state […]
Author: Martin Gugat, Enrique Zuazua, Aleksey Sikstel, FAU DCN-AvH Code: [HINT] To run the software on your computer, you may have to install additional standard software packages (like cmake and a c++ compiler) and additional libraries (lapack, PETSc). In order to optimize the operation of gas transportation networks, […]
Author: Carlos Esteve, Deusto CCM Code: In a previous post “Inverse Design For Hamilton-Jacobi Equations“, described all the possible initial states that agree with the given observation of the system at time on the reconstruction of the initial state in many evolution models. Our goal here is to study the […]
Author: Daniel Veldman, FAU DCN-AvH Code: || Also available @Daniël’s GitHub In a previous post “Randomized time-splitting in linear-quadratic optimal control“, it was proposed to use the Random Batch Method (RBM) to solve classical Linear-Quadratic (LQ) optimal control problems. This contribution is concerned with the corresponding numerical implementation. We thus […]
Author: Alexei Gazca, FAU DCN-AvH Code: Below is a description of the types of problems that can be tackled using the code contained in this repository. Solving linear systems arising from the discretisation of partial differential equations can be an extremely challenging and computationally intensive task, especially for problems […]
Transition Layers in Elliptic Equations Stable transition layers in an unbalanced bistable equation Consider the following semi-linear problem where are positive functions in ; is a positive parameter and We assume that the functions satisfy ; for all ; there is a sub-interval such that for and for all […]
Randomized time-splitting in linear-quadratic optimal control By Daniël Veldman Introduction Solving an optimal control problem for a large-scale dynamical system can be computationally demanding. This problem appears in numerous applications. One example is Model Predictive Control (MPC), which requires the solution of several optimal control problems on a receding […]
Felix Klein: A Legacy of Innovation in Mathematics and Education By Roberto Rodríguez del Río, Complutense University of Madrid | IES San Mateo, Madrid Felix Christian Klein lived in a period of history of science in which Mathematics were involved in a process of transformation, leaving behind the classical […]
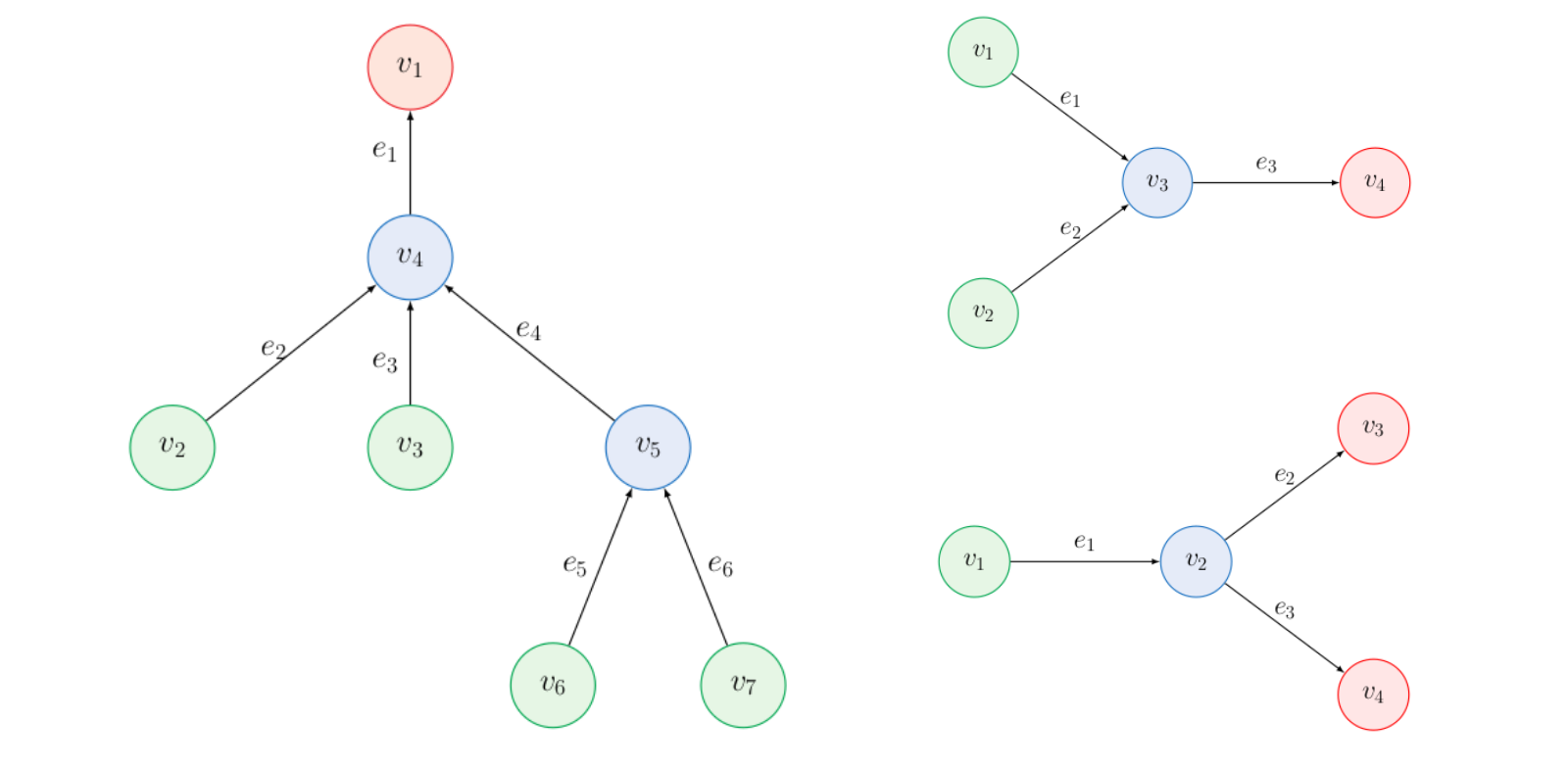
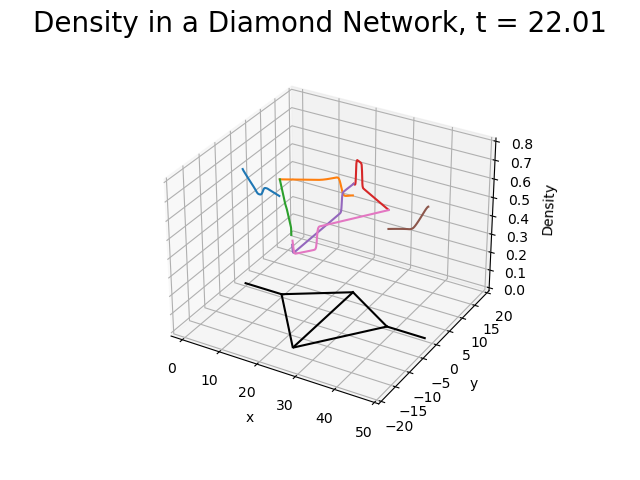
Control of Advection-Diffusion Equations on Networks and Singular Limits By Jon Asier Bárcena-Petisco, Márcio Cavalcante, Giuseppe Maria Coclite, Nicola de Nitti and Enrique Zuazua Introduction In the past few decades, models based on partial differential equations have been very effective in tackling many problems dealing with flows on networks (e.g. […]
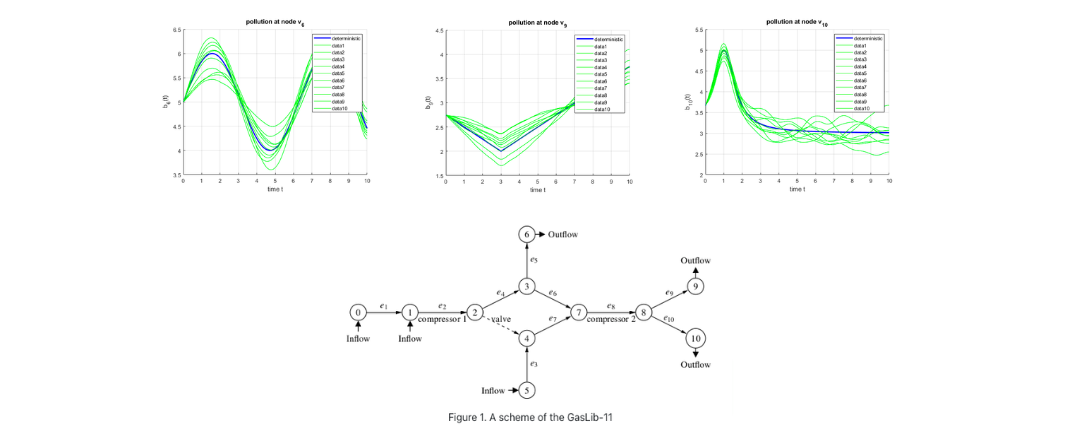
Probabilistic Constrained Optimization on Flow Networks This research was funded by DFG in the SFB Transregio 154: Mathematical modelling, simulation and optimization using the example of gas networks. Uncertainty often plays an important role in the context of flow problems. We analyze a stationary and a dynamic flow model […]
Perceptrons, Neural Networks and Dynamical Systems By Sergi Andreu // This post is last part of the “Deep Learning and Paradigms” post Binary classification with Neural Networks When dealing with data classification, it is very useful to just assign a color/shape to every label, and so be able to visualize data in a lower-dimensional […]
Deep Learning and Paradigms By Sergi Andreu // This post is the 2nd. part of the “Opening the black box of Deep Learning” post Deep Learning Now that we have some intuition about the data, it’s time to focus on how to approximate the functions that would fit that data. […]
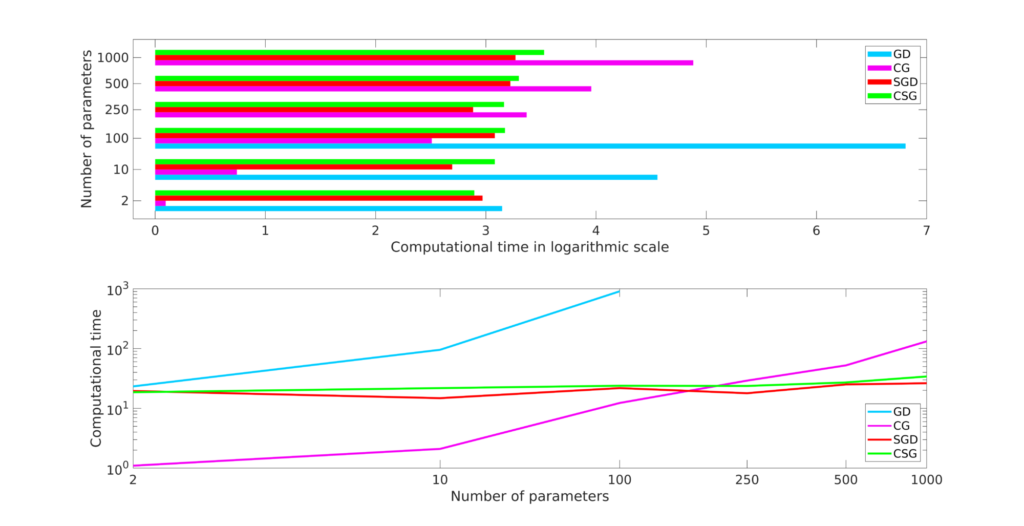
Opening the black box of Deep Learning By Sergi Andreu Deep Learning is one of the three main paradigms of Machine Learning, and roughly consists on extracting patterns from data using neural networks. Its impact in modern technologies is huge. However, there is not a clear high-level description of what […]
Averaged dynamics and control for heat equations with random diffusion By Jon Asier Bárcena Petisco, Enrique Zuazua Background and motivation Let us consider the random heat equation described by the following system: for a domain, a subdomain, a control, the initial configuration and the diffusivity coefficient, which is a positive […]
pyGasControls Framework By Martin Gugat, Enrique Zuazua, Aleksey Sikstel In order to optimize the operation of gas transportation networks, as a first step a powerful simulation software is mandatory. The flow model from continuum mechanics leads to a nonlinear hyperbolic system of balance laws for each pipe. For the dynamics […]
Model-based optimization of ripening processes with feedback modules By Michele Spinola 1 Important remark This contribution presents a proof of concept together with numerical results to obtain a first idea how to deal with specific process chains within chemical engineering. The main reference of this webpage entry is [1]. Furthermore, […]
Gas networks uncertainty and Probust constraints: model, distribution and optimization By Martin Gugat Gas transport and distribution systems are usually operating under complex pipelines network topologies which make possible gas flow over interconnected stations -nodes- and branches under a variety of conditions, especially large-scale gas infrastructures. As many applications contain […]
Q-learning for finite-dimensional problems By Carlos Esteve Reinforcement Learning Reinforcement Learning (RL) is, together with Supervised Learning and Unsupervised Learning, one of the three fundamental learning paradigms in Machine Learning. The goal in RL is to enhance the manipulation of a controlled system by using data from past experiments. […]
The interplay of control and Deep Learning By Borjan Geshkovski It is superfluous to state the impact deep (machine) learning has had on modern technology, as it powers many tools of modern society, ranging from web searches to content filtering on social networks. It is also increasingly present in […]
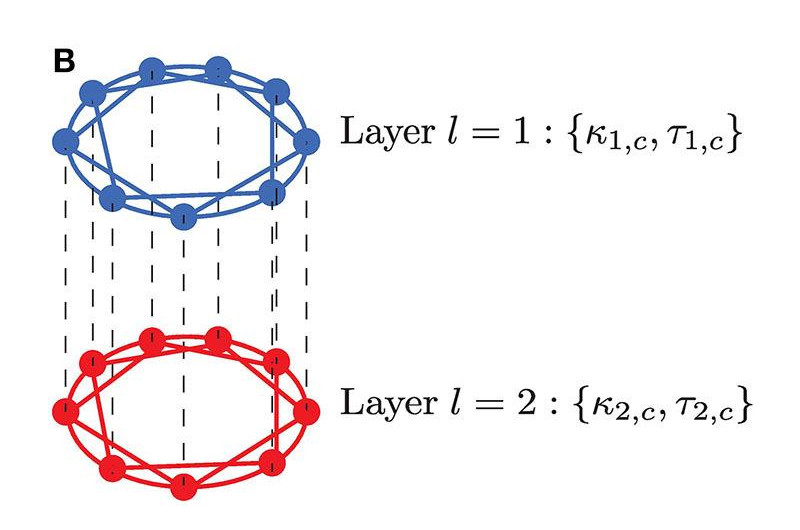
Neural networks and Machine Learning By Marius Yamakou Neural Networks with time delayed connections Neurons communicate with each other through electrical signals. It is well known that these signals are oscillatory and that the properties of the oscillations depend on the characteristics of the individual neurons, how the neurons are […]
Stochastic Synchronization of Chaotic Neurons By Marius Yamakou Real biological neurons can show chaotic dynamics when excited by the certain external input current. The behavior of these neurons is characterized by instability and, as a result, limited predictability in time. Mathematically, a system is chaotic if it has a […]
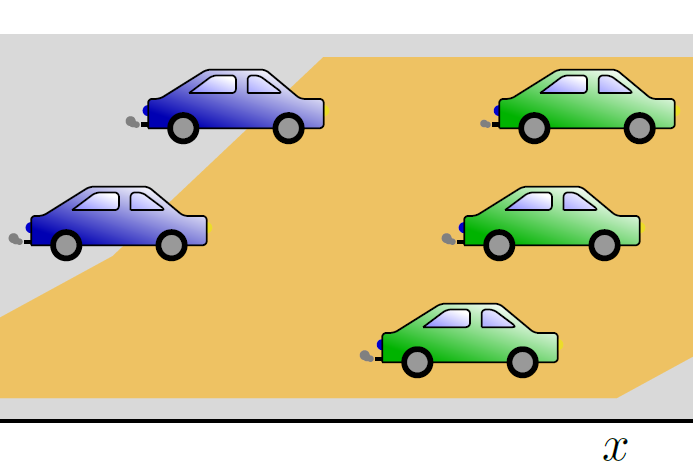
Nonlocal population balance equations and applications By Michele Spinola Motivational example: look ahead behavior of car drivers When analyzing traffic situations, one possible way to observe the current state is from bird’s eye view. The velocity of a car driver at time at location depends on the traffic density at […]
Inverse Design For Hamilton-Jacobi Equations By Carlos Esteve, Enrique Zuazua In many evolution models, the reconstruction of the initial state given an observation of the system at time represents a major challenge in mathematical modelling. Especially if it involves irreversible processes, where sometimes, different initial conditions can lead the system […]
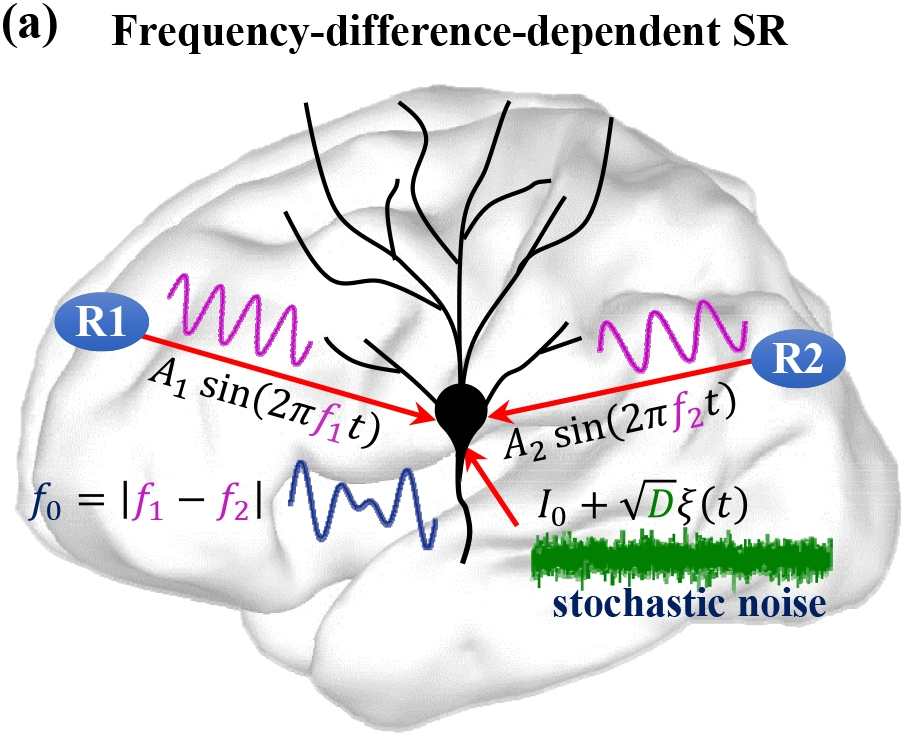
Stochastic Neural Dynamics By Marius Yamakou Neural activity shows fluctuations and unpredictable transitions in its dynamics. This randomness can be an integral aspect of neuronal function; examples range from discrete fluctuations of ion channels to sudden sleep stage transitions involving the entire brain. To understand brain function as well as […]
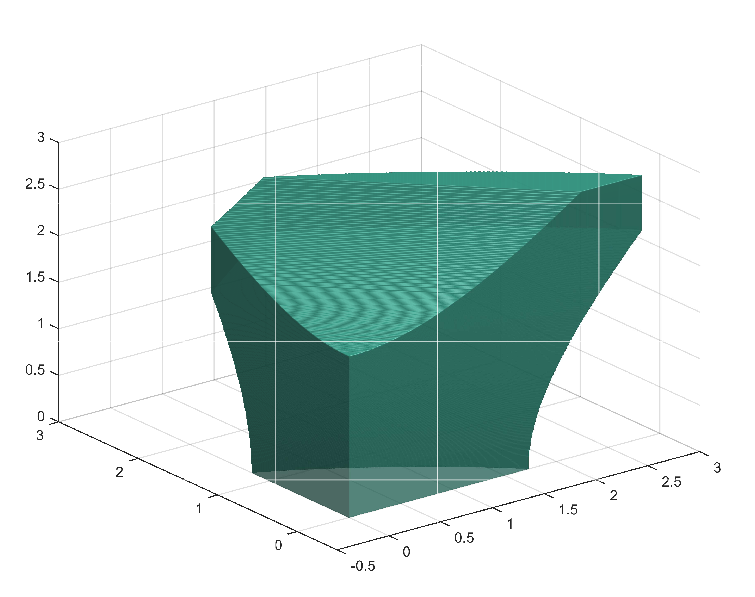
Controllability properties of fractional PDE By Umberto Biccari Controllability of the fractional heat equation Let be an open and nonempty subset. Consider the following non-local one-dimensional heat equation defined on the domain where is a given initial datum. In (1), for all , denotes the one-dimensional fractional Laplace operator, […]
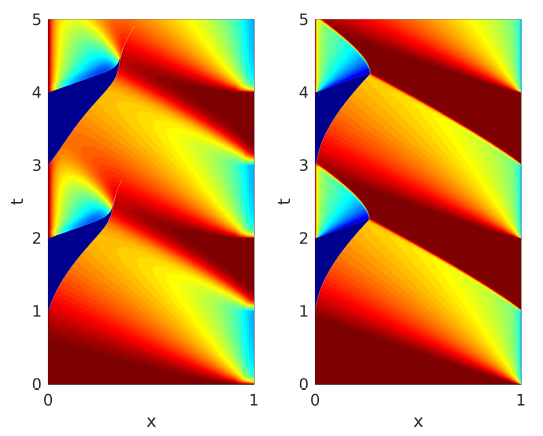
Flows on Networks By Enrique Zuazua, Nicola de Nitti PDE models on Networks In the last few decades, models based on partial differential equations have been very effective in tackling many applied problems dealing with flows on networks. The areas of application include mainly the study of vehicular traffic, […]
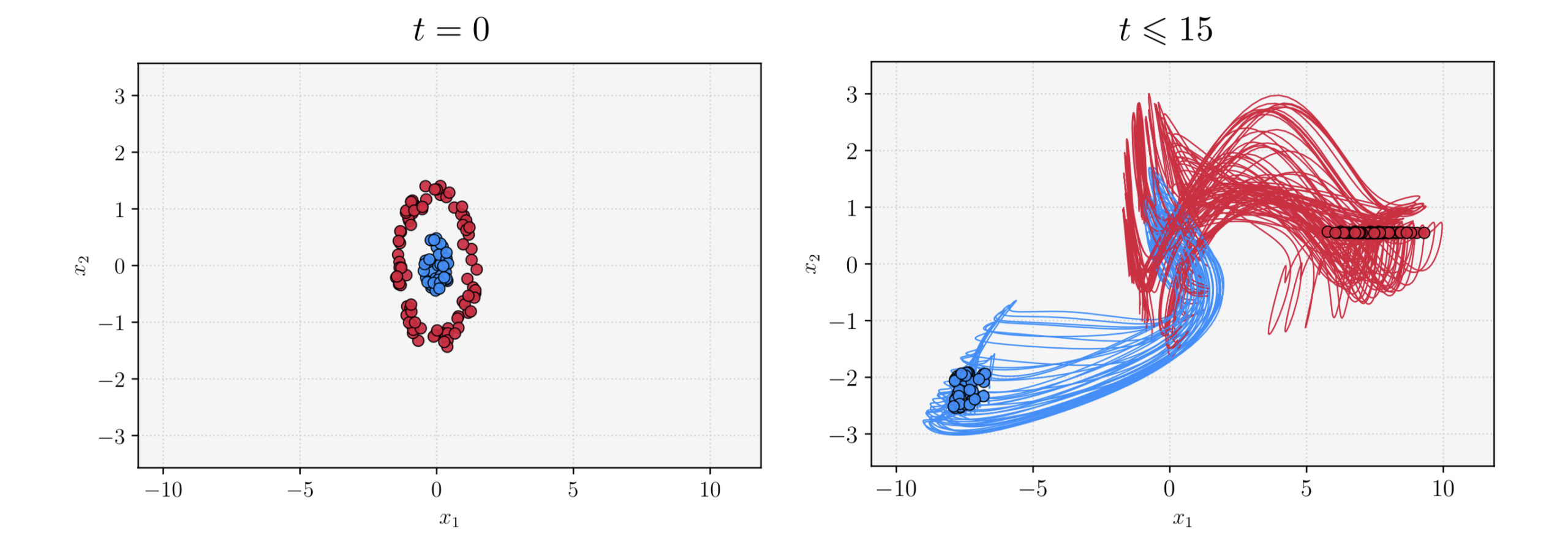
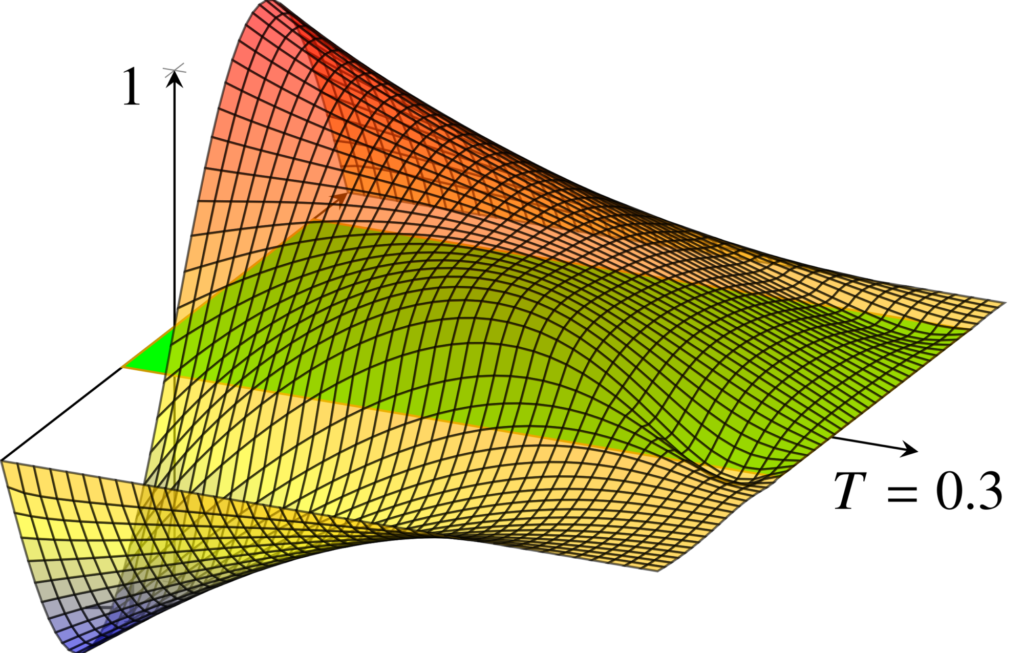
Stochastic optimization for simultaneous control By Umberto Biccari What is a simultaneous control problem? Consider the following parameter-dependent linear control system with The matrix is associated with the Brunovsky canonical form of the linear ODE where denotes the -th derivative of the function . In (1)-(2), , , […]
Convexity and Starshapedness of feasible sets in Stationary Flow Networks This research was funded by DFG in the SFB Transregio 154: Mathematical modelling, simulation and optimization using the example of gas networks. Uncertainty often plays an important role in application driven modeling. This often leads to optimization problems […]
Collective dynamics modelling, Control and Simulation By Dongnam Ko Collective dynamics Herds, packs, bird flocks, and fish schools are common examples of the collective behaviors arising from the interactions of individuals. Each individual has its own decision policy, as in the stock market or game theory, which interacts with […]
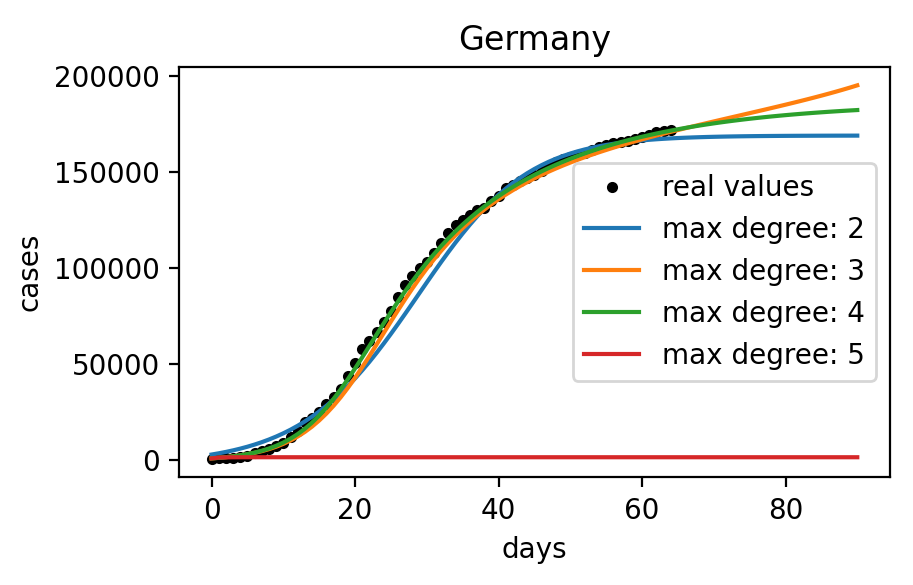
Classical models By Cyprien Neverov Compartmental epidemiological models [1] where introduced almost a century ago and are still considered the standard way of modeling a disease in a population. They are also called SIR models because they divide the population into different compartments like Susceptible, Exposed, Infected, Recovered and model […]
Non-local population balance equations By Michele Spinola Nichtlokale Populationsbilanzgleichungen. Der Verlauf des Weges wie zur Schule oder zur Arbeit hängt stark von der entsprechenden Verkehrslage ab. Genauso spielen chemisch synthetisierte Produkte wie Pharmaka oder Kosmetika eine wichtige Rolle im Alltag. Dementsprechend relevant ist es, mathematische Modelle zu entwickeln, die diese […]