Introduction The Lotka-Volterra model reflects real ecological interactions where species compete for limited resources, potentially leading to coexistence, dominance of one species, or extinction of another. Comprehending the mechanisms governing these systems can yield critical insights for developing strategies in ecological management and biodiversity conservation. In this post, we […]
Math
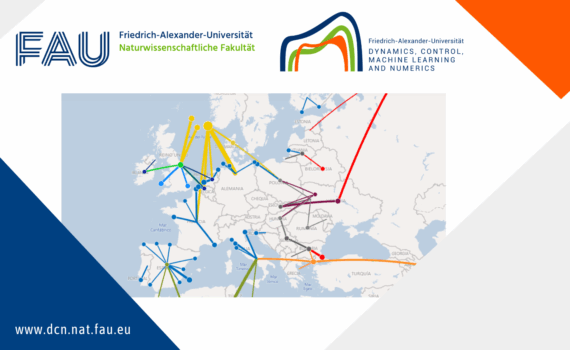
Mathematical modeling and numerical simulations for Gas Dynamics (on Networks) Gas transport networks are essential in the real world, e.g, energy supply, industrial applications, and emergency services. In our model, we focus on the gas flow of pipeline networks that are described by the Euler equations, which are given by […]
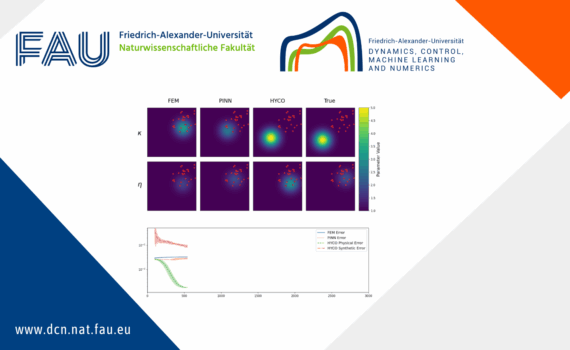
HYCO: The hybrid-collapse strategy for time-independent PDEs This post explores core ideas on a novel hybrid modelling procedure, within the framework of time-independent partial differential equations, drawn from ongoing research in collaboration with Lorenzo Liverani and Enrique Zuazua. GitHub Repository The code to reproduce the experiments can be found at […]
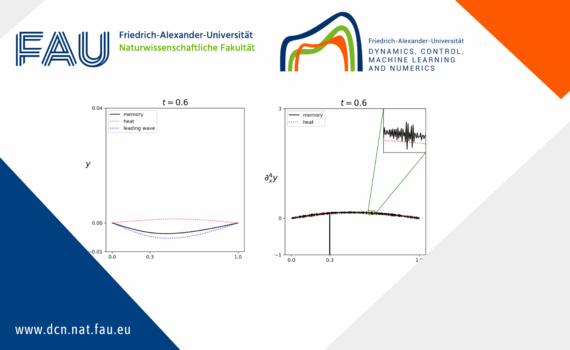
Hybrid parabolic-hyperbolic effect for heat equations with memory 1 Introduction PDEs with memory involve the past values of solutions. In the modeling, one physical quantity induces time-delayed actions on others, and and a large number of such actions form memory (as a time integral). Such models with memory are […]
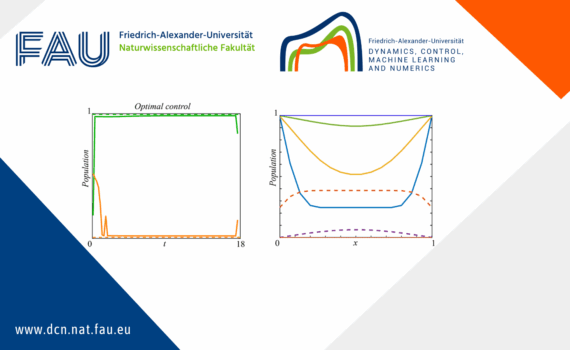
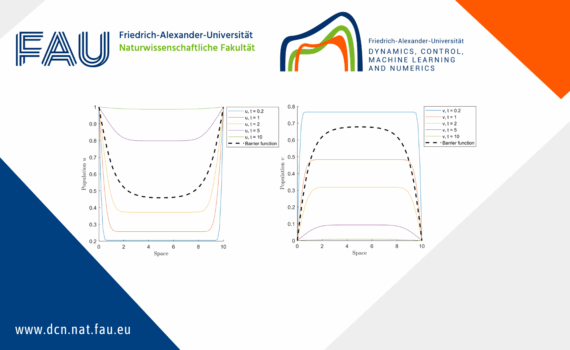
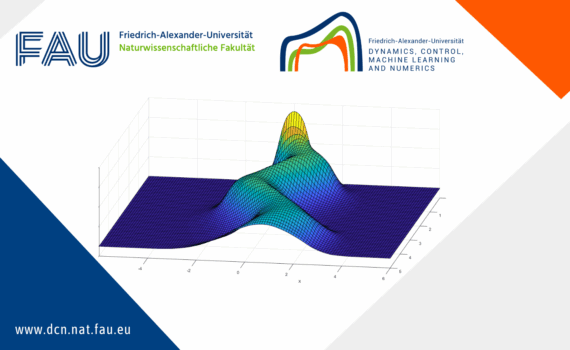
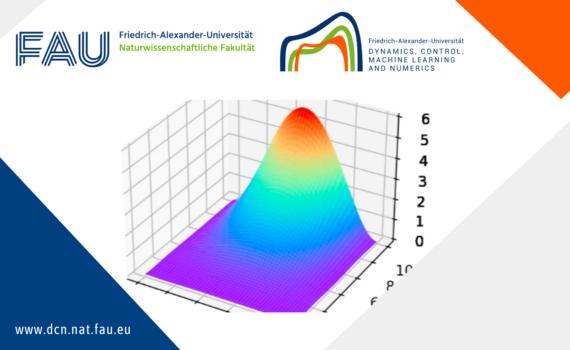
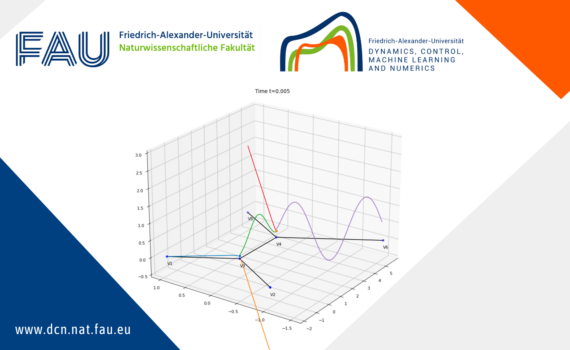
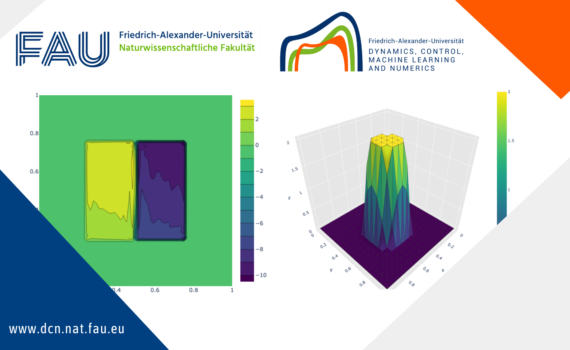
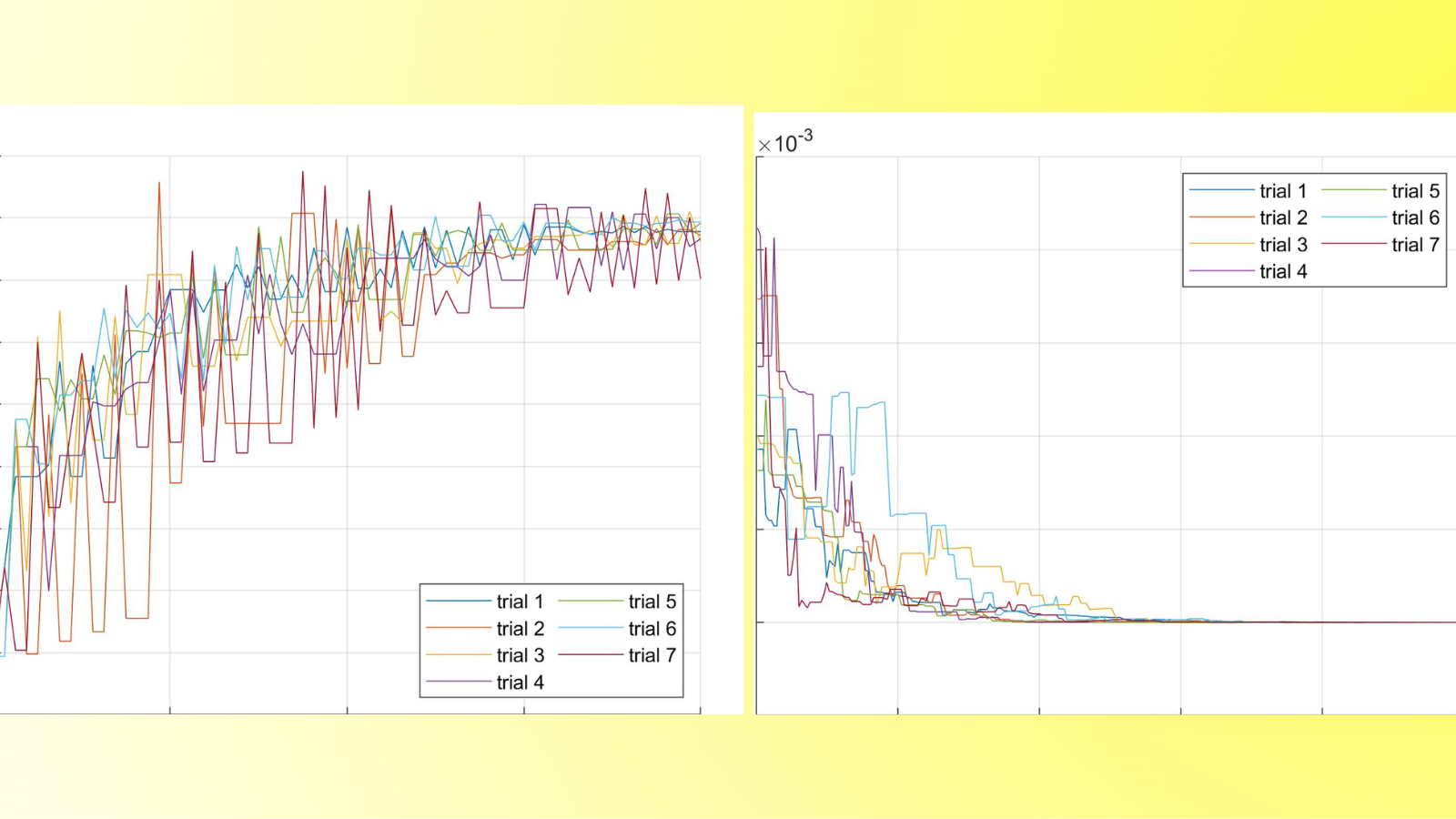
Boundary and Interior Control in a Diffusive Lotka-volterra Model 1 Introduction 1.1 Problem formulation and main results In this post, we consider a general diffusive Lotka-Volterra Model (LVM) for two competing species. The system, with boundary controls and an interior multiplicative control, is described by where are positive parameters, […]
Optimal control of Fokker-Planck and transport equations using renormalized solutions 1 Introduction The fundamental general optimal control problem we consider is the following: This is a bilinear optimal control problem for a Fokker-Planck equation (1.1) with time-dependent control . In the objective function to be minimized, with are weighting […]
Mathematics & Philosophy: On the philosophical foundations of mathematics and its role as a structural science When we talk about mathematics today, many people think primarily of numbers, formulas, and calculations. Yet anyone who delves more deeply into the field soon discovers that mathematics is far more than a mere […]
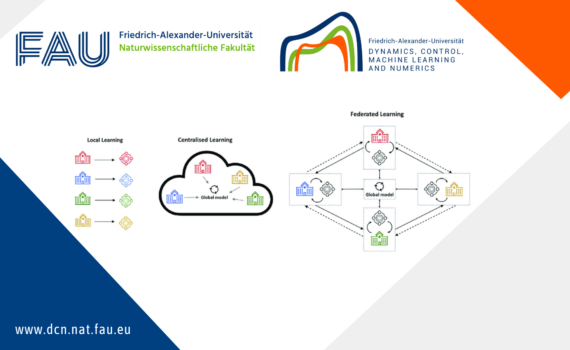
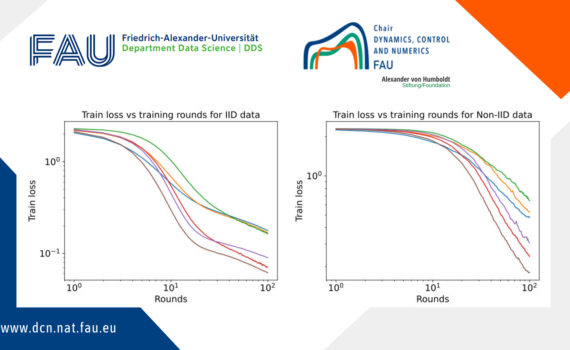
Federated Learning for Systems Identification Federated learning (FL) operates in a decentralized manner, as shown Figure 1, allowing multiple clients (or devices) to collaboratively train a model while ensuring the privacy of local data. This method is particularly relevant for systems identification, where clients have access to limited and environmentspecific […]
3−wave turbulence kinetics: Numerical approach for energy cascading This post provides an overview of the results presented in the paper “Numerical schemes for a fully nonlinear coagulation-fragmentation model coming from wave kinetic theory” by Arijit Das and Minh-Binh Tran [1]. 1. Introduction The theory of wave turbulence has been […]
How to steer a fleet of agents by controlling only a few: a mean-field approach 1 Introduction The challenge of controlling large systems of interacting agents has garnered significant attention in recent years. Applications of such problems include crowd evacuations, achieving consensus within a large group, and traffic flow […]
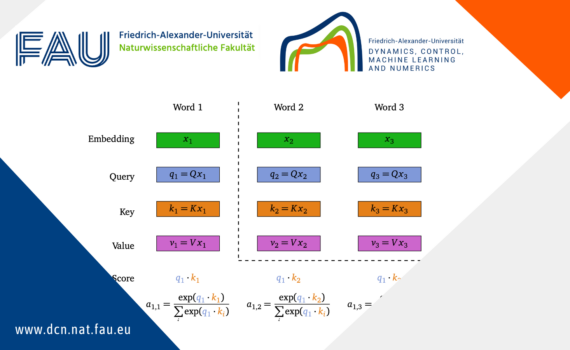
Clustering in discrete-time self-attention Since the article Attention Is All You Need [1] published in 2017, many Deep Learning models adopt the architecture of Transformers, especially for Natural Language Processing and sequence modeling. These Transformers are essentially composed of layers, alternating between self-attention layers and feed forward layers, with normalization […]
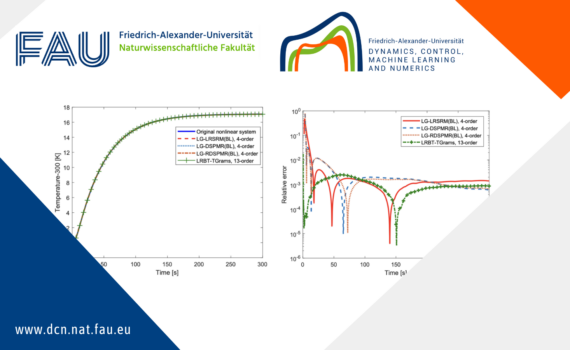
Low-rank balanced truncation of bilinear systems via Laguerre functions 1 Introduction Bilinear systems are an important class of nonlinear systems which typically arise from approximating more involved nonlinearities by using the Carleman linearization approach or by imposing certain boundary conditions to discretized partial differential equations (PDEs). They can be […]
Generalization bounds for neural ODEs: A user-friendly guide Once a neural network is trained, how can one measure its performance on new, unseen data? This concept is known as generalization. While many theoretical models exist, practical models often lack comprehensive generalization results. This post introduces a probabilistic approach to quantify […]
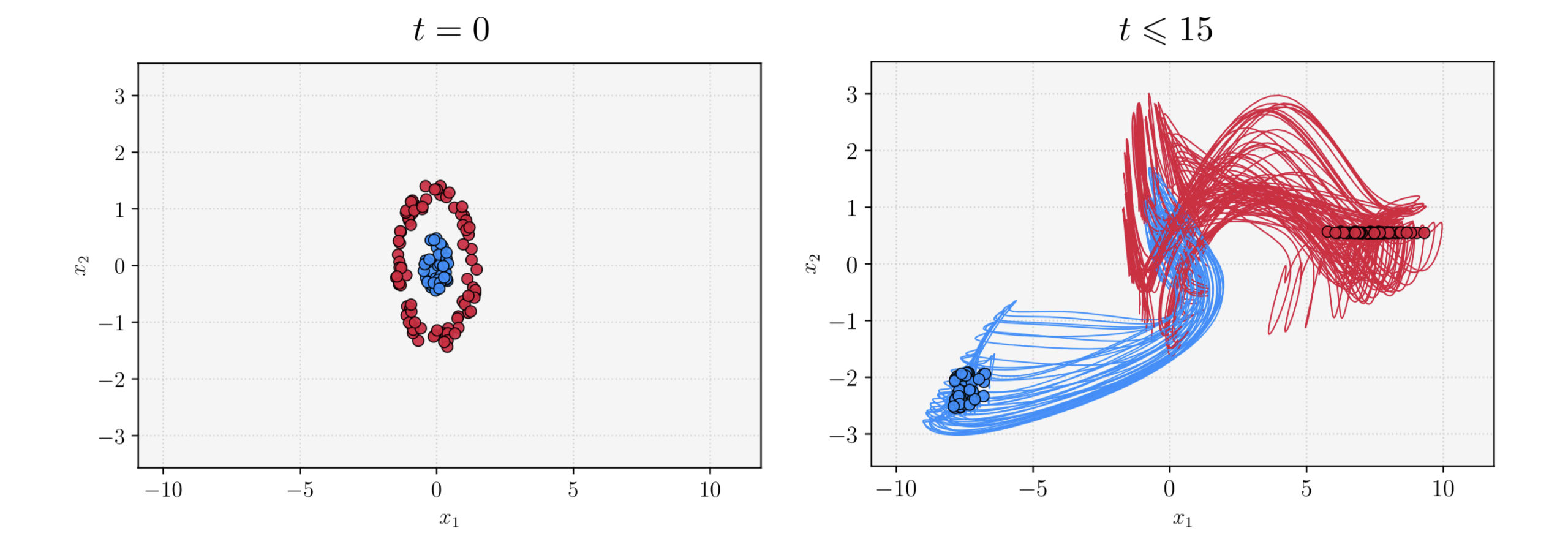
Clustering in pure-attention hardmax transformers and its role in sentiment analysis This post provides an overview of the results in the paper Clustering in Pure-Attention Hardmax Transformers and its Role in Sentiment Analysis by Albert Alcalde, Giovanni Fantuzzi, and Enrique Zuazua [1]. Codes used to reproduce the simulations can be […]
Partially dissipative hyperbolic systems without Fourier analysis 1 Models We study the large-time behavior of the one-dimensional partially dissipative hyperbolic system where () is the vector-valued unknown, is a smooth matrix-valued symmetric function and is a positive semidefinite symmetric matrix. System (1.1) models non-equilibrium processes in physics for media […]
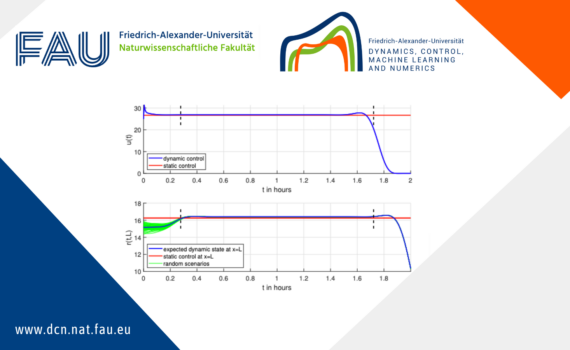
A Turnpike Result for Optimal Boundary Control Problems with the Transport Equation under Uncertainty 1 The Deterministic Optimal Control Croblem We consider a deterministic optimal boundary control problem governed by a linear transport equation with source term and the corresponding static optimal problem. We state an integral turnpike result […]
PINNs Introductory Code for the Heat Equation This repository provides some basic insights on Physics Informed Neural Networks (PINNs) and their implementation. PINNs are numerical methods based on the universal approximation capacity of neural networks, aiming to approximate solutions of partial differential equations. Recently, extensive focus has been on approximating […]
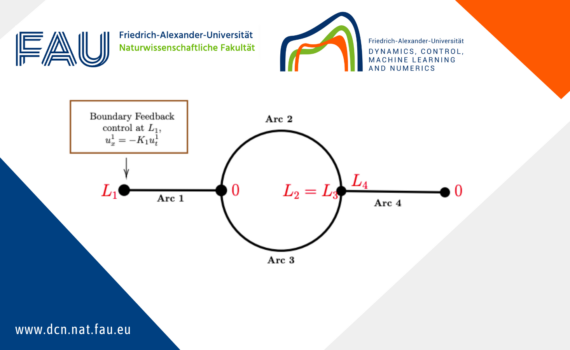
Limits of the stabilization of a networked hyperbolic system with a circle 1 Introduction In this post, we discuss the exponential stability of a networked hyperbolic system with a circle. In many applications, the graphs of these networks contain cycles, such as pipeline networks for gas transportation (see, for example, […]
Stability of hyperbolic systems with non-symmetric partial dissipation Introduction In this post, we report new results for -components linear hyperbolic systems in of the type The unknown () depends on the time variable and on the space variable , is a symmetric matrix and is a semidefinite positive matrix […]
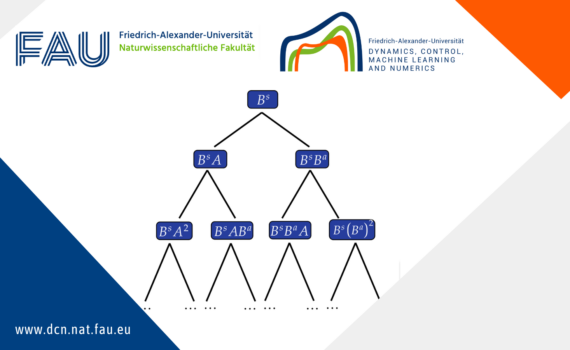
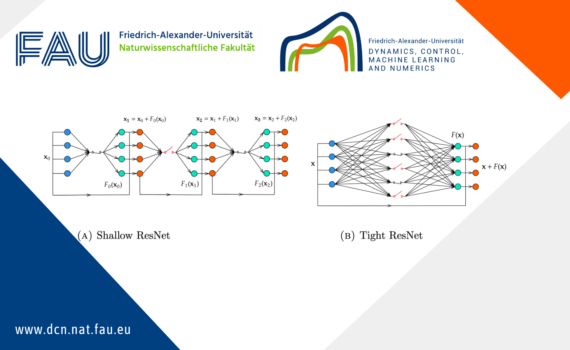
Neural ODEs for interpolation and transport: From tight to shallow Introduction We consider in our work residual neural networks (ResNets) which take the form for some initial input . The states are the output after each layers, with being the final output. The depth of the neural network is the […]
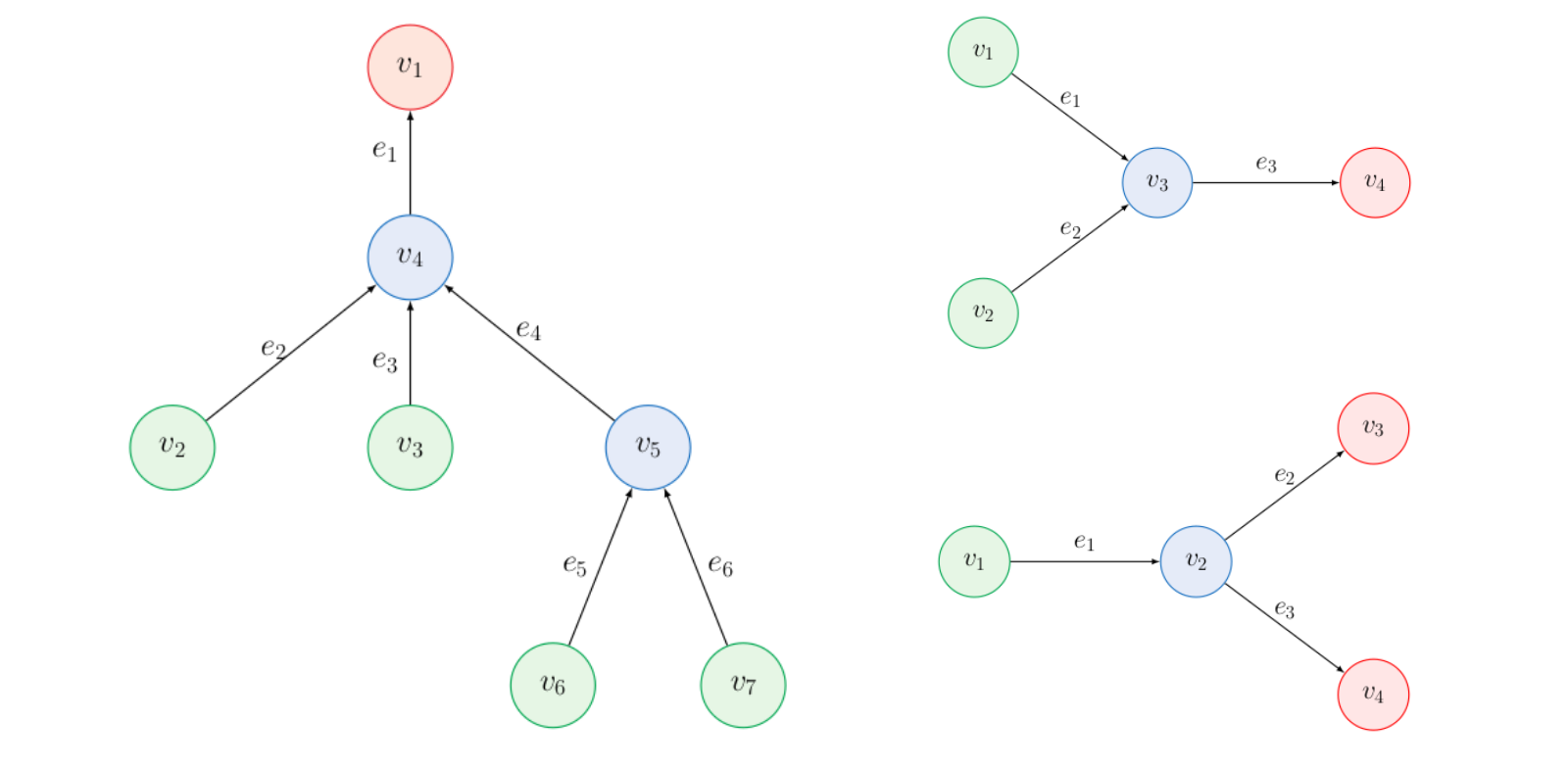
Combined convection and diffusion in a network. A numerical analysis. The problem: a contaminant in a network of water pipes Imagine that there is a network of pipes full of water. The water is flowing from some source nodes (say, some water plants) to some destination nodes (say, people’s homes). […]
The ADMM-PINNs Algorithmic Framework for Nonsmooth PDE-Constrained Optimization: A Deep Learning Approach Motivation This post shows the source code from the paper “The ADMM-PINNs Algorithmic Framework for Nonsmooth PDE-Constrained Optimization: A Deep Learning Approach”. (See reference below) We study the combination of the alternating direction method of multipliers (ADMM) with […]
Reinforcement learning as a new perspective into controlling physical systems Introduction Optimal control addresses the problem of bringing a system from an initial state to a target state, like a satellite that we want to send into orbit using the least possible amount of fuel. Since the last century, mathematics […]
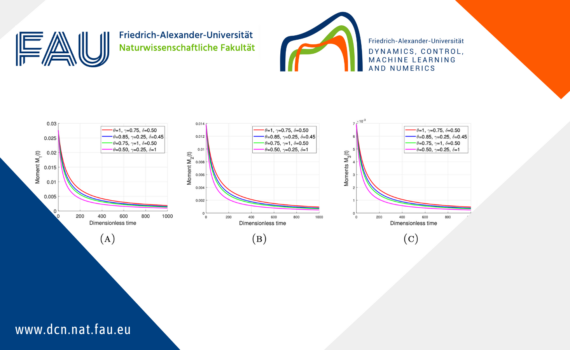
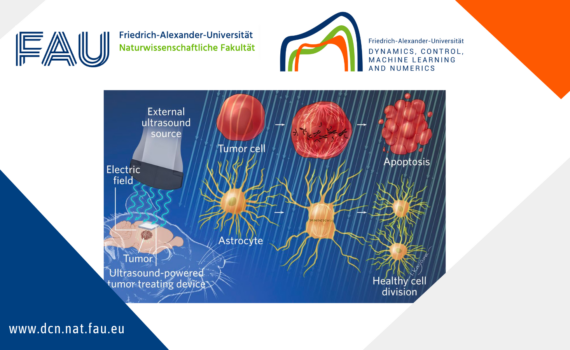
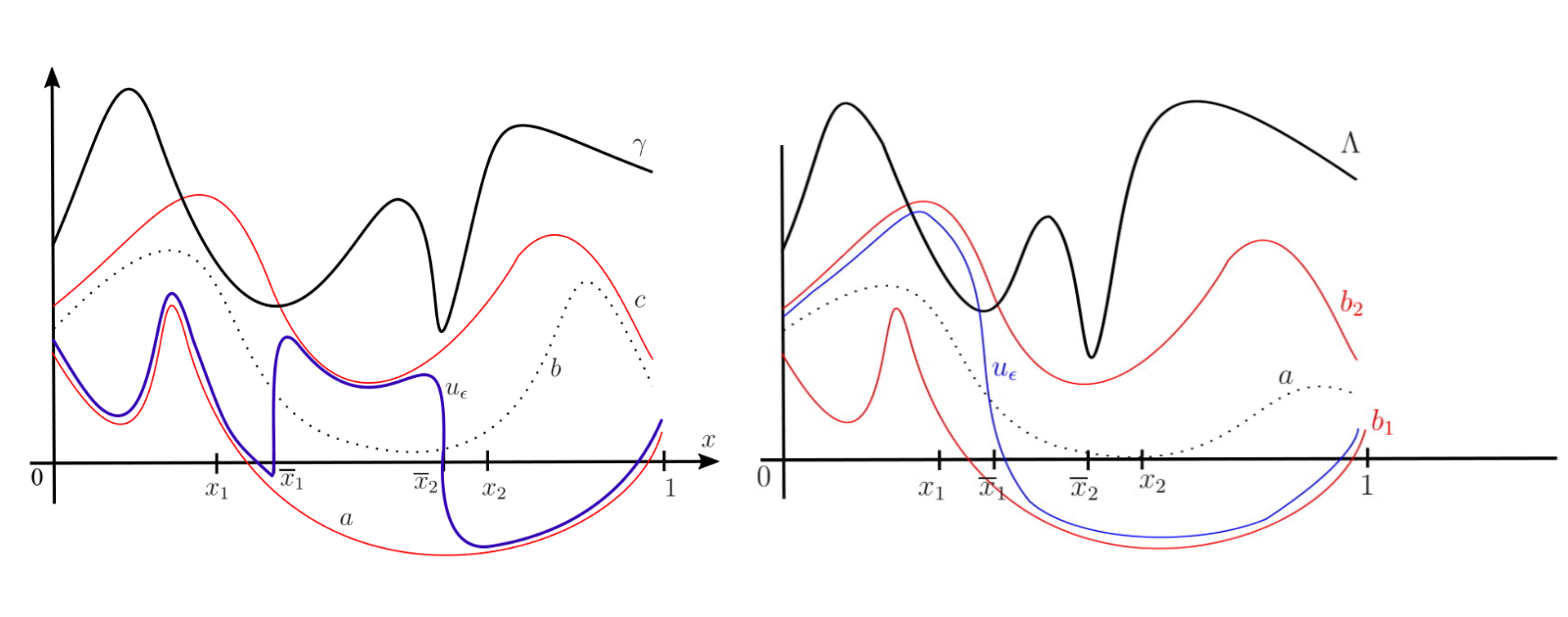
Null controllability for population dynamics with age, size structuring and diffusion 1. Motivation and description of age, size structured model 1.1. Motivation Knowing the mechanisms of tumor growth can be useful for developing treatments. To mathematically describe its evolution from a global point of view, we can use a so-called […]
Breaking the symmetry with Robin boundary conditions Introduction Establishing symmetry properties of solutions to differential equations is a very important task in mathematical analysis, both from the theoretical point of view and for applications. Indeed, partial differential equations arise in modeling many phenomena in physics, mechanics, and so on. A […]
Convolutional autoencoders for very low-dimensional parametrizations of nonlinear fluid flow 1. Introduction The control of large-dimensional nonlinear dynamical systems is a challenging task because of the 1. system’s size that means a high demand in computational resources 2. and the nonlinearity that adds model inherent complexity to be resolved by […]
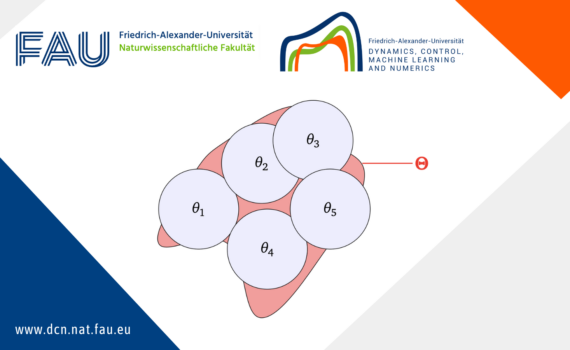
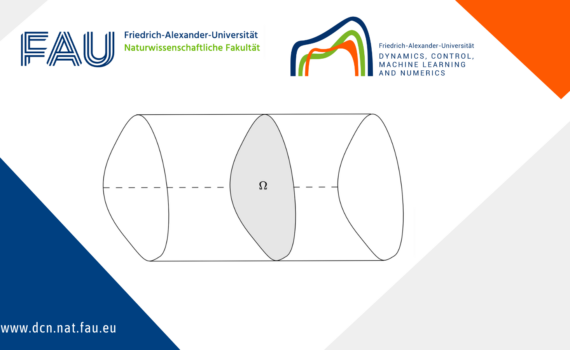
Torsional Rigidity: Classical and new results Torsional rigidity is a key quantity to characterize how a beam responds to applied forces. The higher the torsional rigidity, the harder it is to deform the beam. A natural question arises: which shape for the beam’s cross section yields the highest torsional rigidity? […]
Federated Learning: Protect your data and privacy Code: A basic PyTorch implementation of the FedAvg algorithm (GitHub) Federated Learning is becoming an increasingly popular topic in machine learning. But what is it, and why do we need it? To explain what the excitement is all about, this post outlines the […]
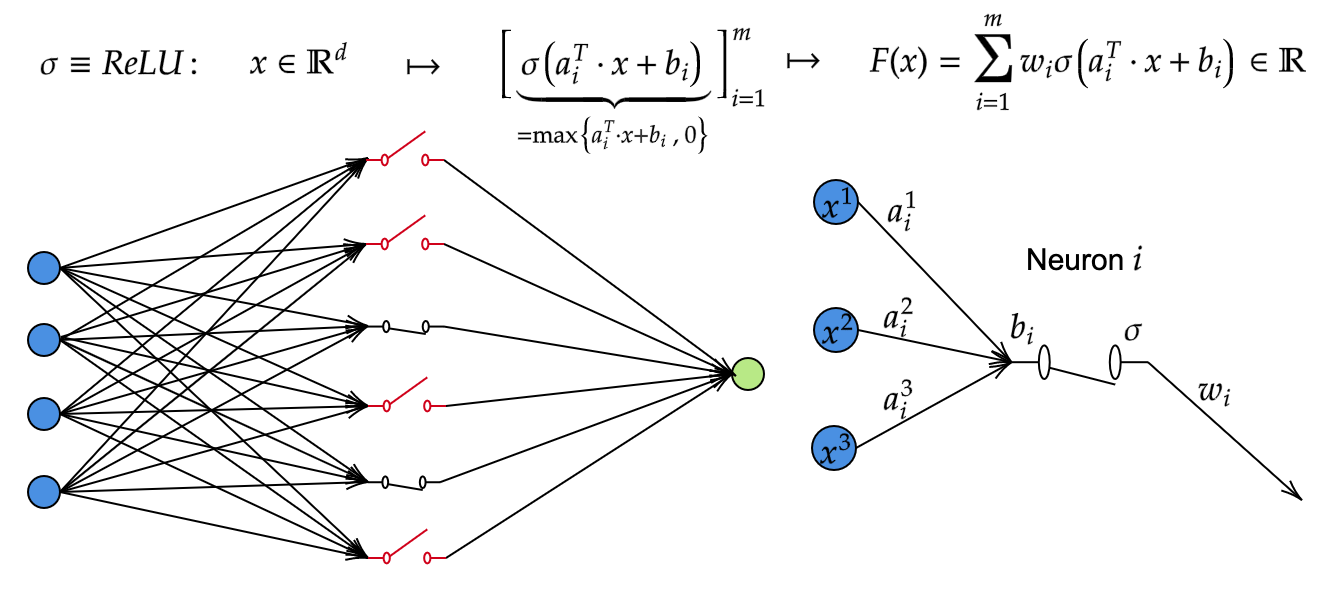
Breaking the curse of dimensionality with Barron spaces 1 Introduction Recent advances in computational hardware have enabled the implementation of the set of algorithmic methods known as Deep Learning, whose development nevertheless dates back several decades. In this way, they have emerged in the latest years as the main tool […]
Stability results for the KdV equation with time-varying delay Introduction The Korteweg-de Vries equation (KdV), is a third-order nonlinear one-dimensional equation given by . It was introduced in [6] to model the propagation of long water waves in a channel. In the last few years, the controllability and stabilization properties […]
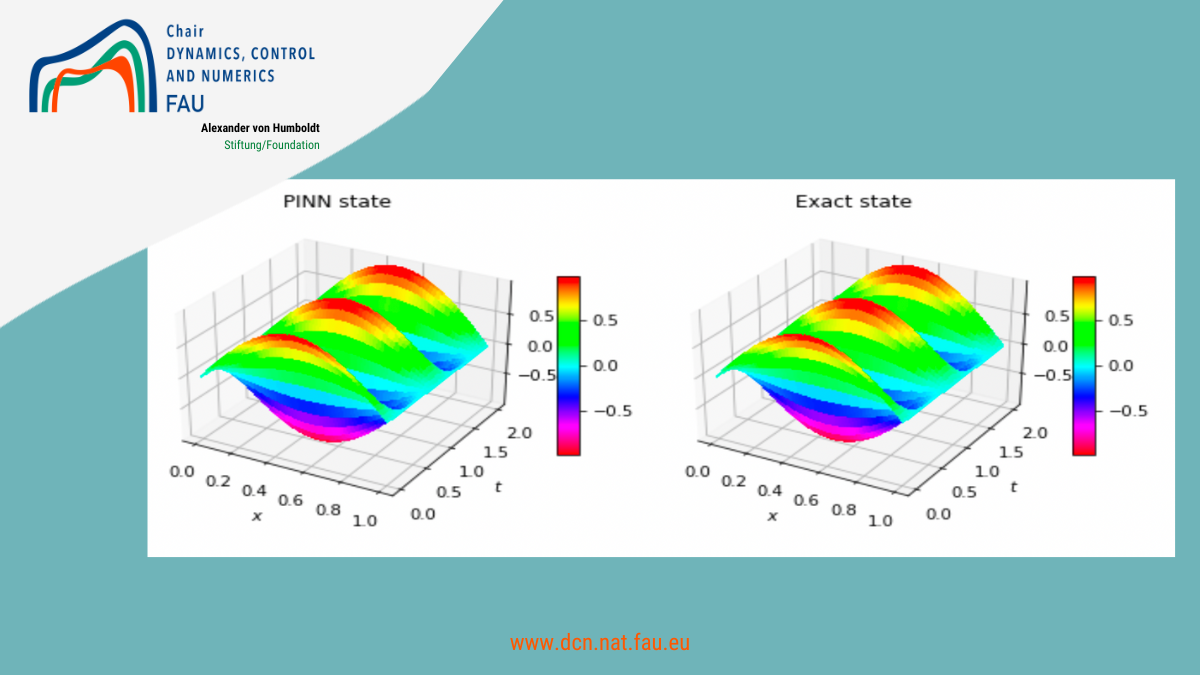
Approximating the 1D wave equation using Physics Informed Neural Networks (PINNs) Introduction Accurate and fast predictions of numerical solutions are of significant interest in many areas of science and industry. On one hand, most theoretical methods used in the industry are the result of deriving differential equations that are […]
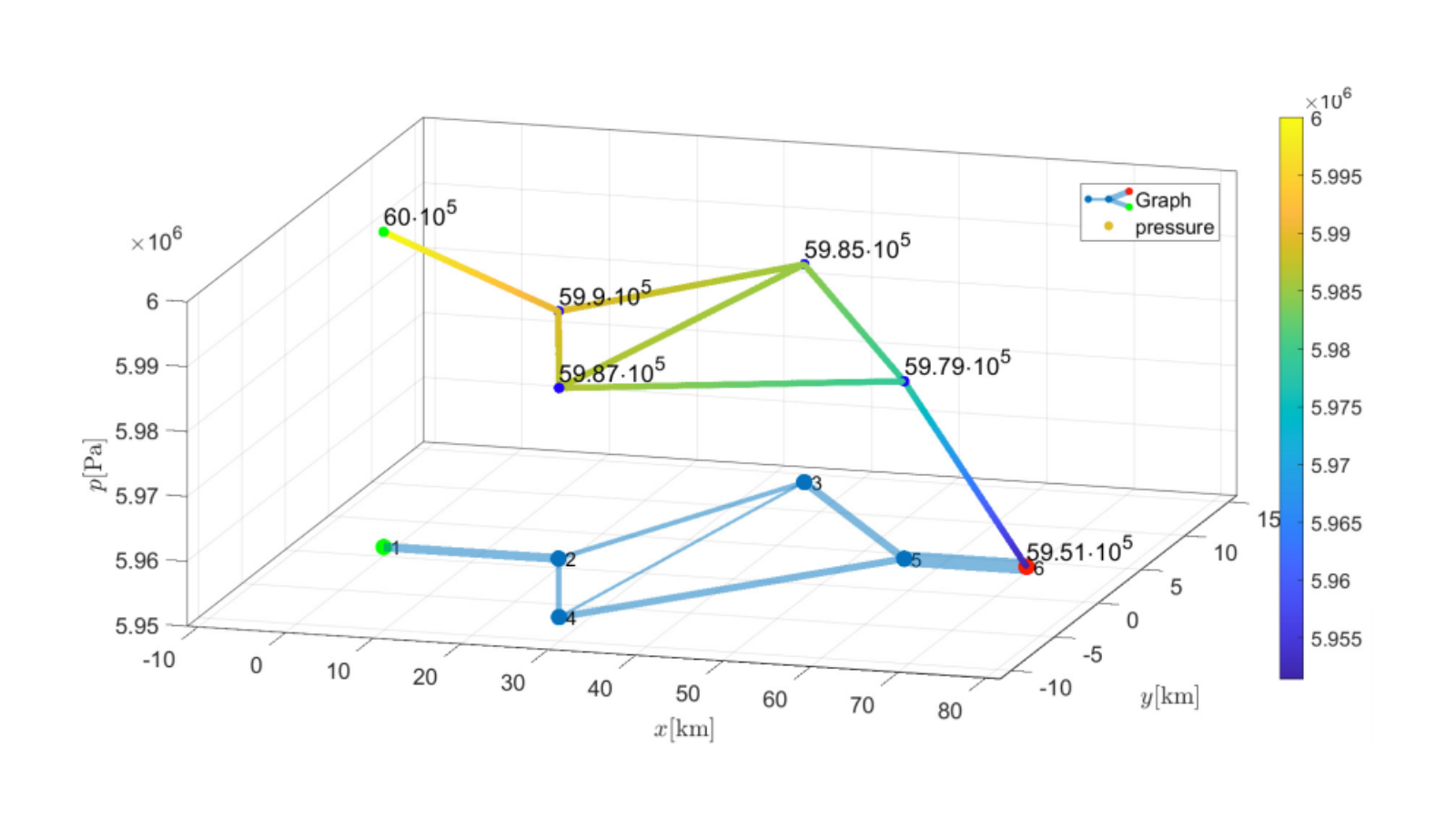
Gas networks at stationary states: Analysis, software and visualization Code: Files to run: nocircle.m, onecircle.m or twocircles.m 1 Introduction This post presents the results of my Bachelor thesis about the modeling and implementation of gas networks at stationary states. Using the isothermal Euler equations to describe the gas flow […]
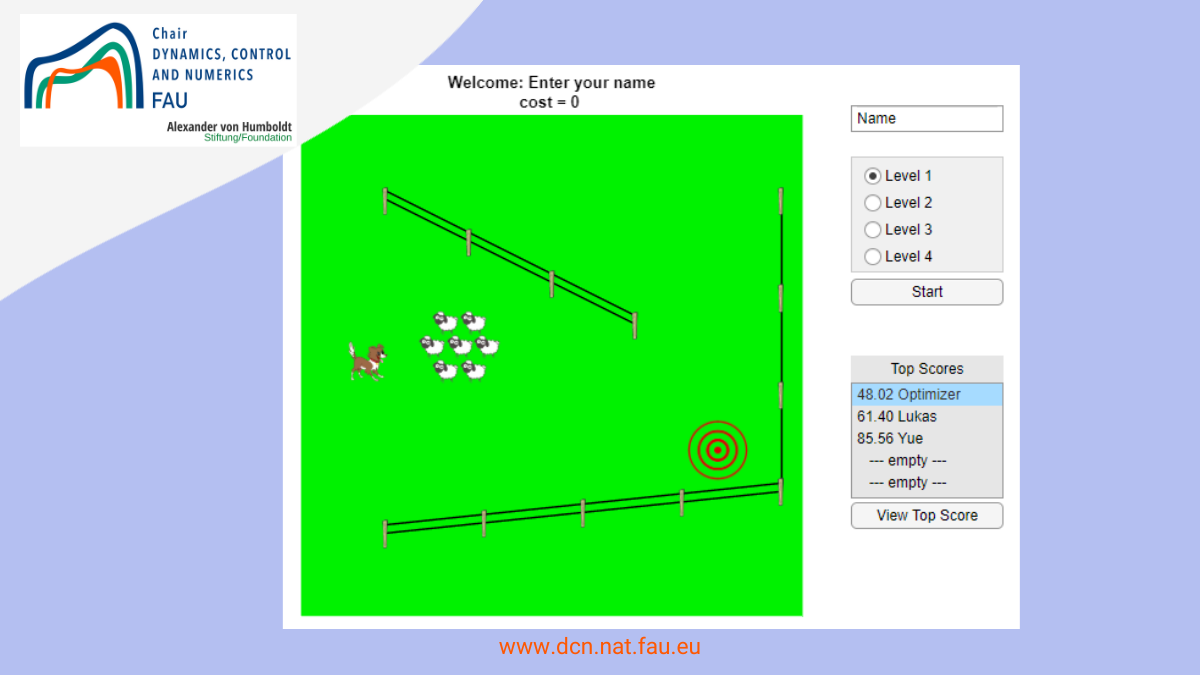
Author: Daniël Veldman, FAU DCN-AvH Code: A sheep herding game in MATLAB developed for the Long Night of Science #NdW22 (Lange Nacht der Wissenschaft) Erlangen-Furth-Nuernberg 2022. Main rules • The dog should drive sheep to the target (red). • You can steer the dog with the arrow keys. • The […]
Author: Martín Hernández, FAU DCN-AvH Code: In this repository, we show a code for Lloyd’s algorithm. Also called Voronoid iteration, this is an iterative algorithm finding for equispaced convex cells in euclidean space. Lloyd’s algorithm finds the distribution of the cells computing their center of mass and iteratively applying the […]
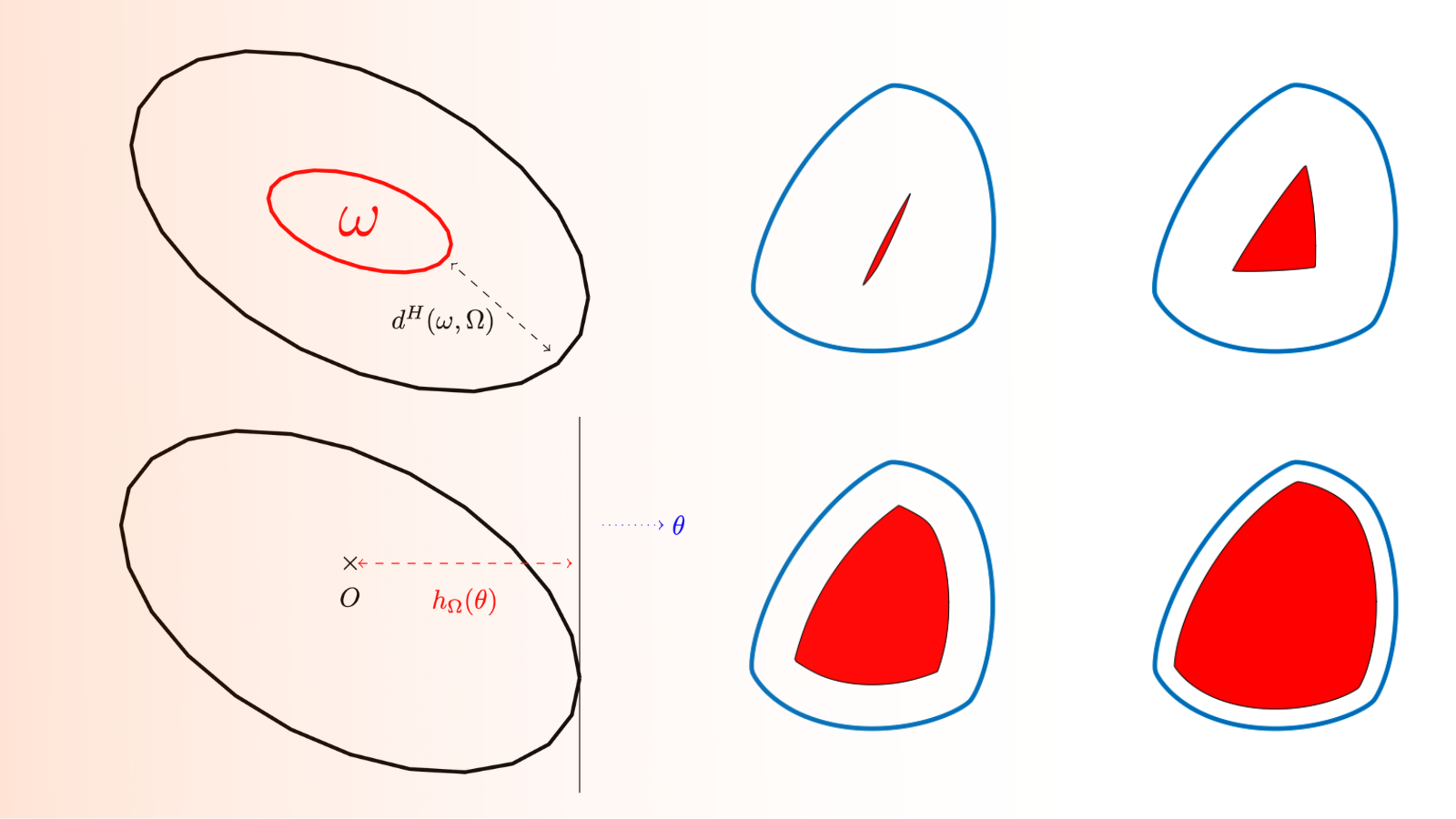
Using the support function for optimal shape design 1 Motivation Led by problems of optimal placement and design of sensors, we are interested in considering the following shape optimization problem where is the Hausdorff distance between and defined as follows with is the distance from to the set . […]
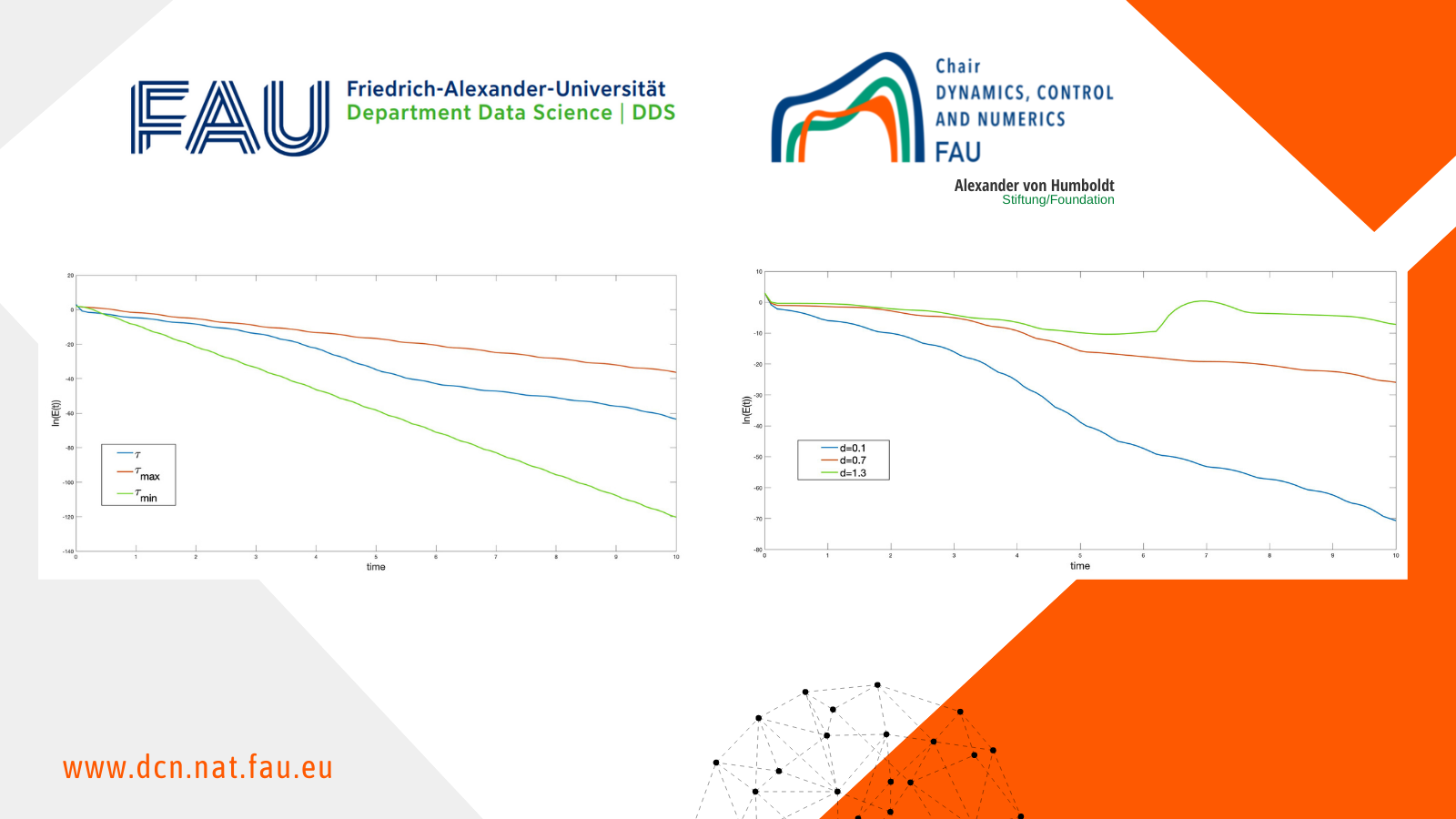
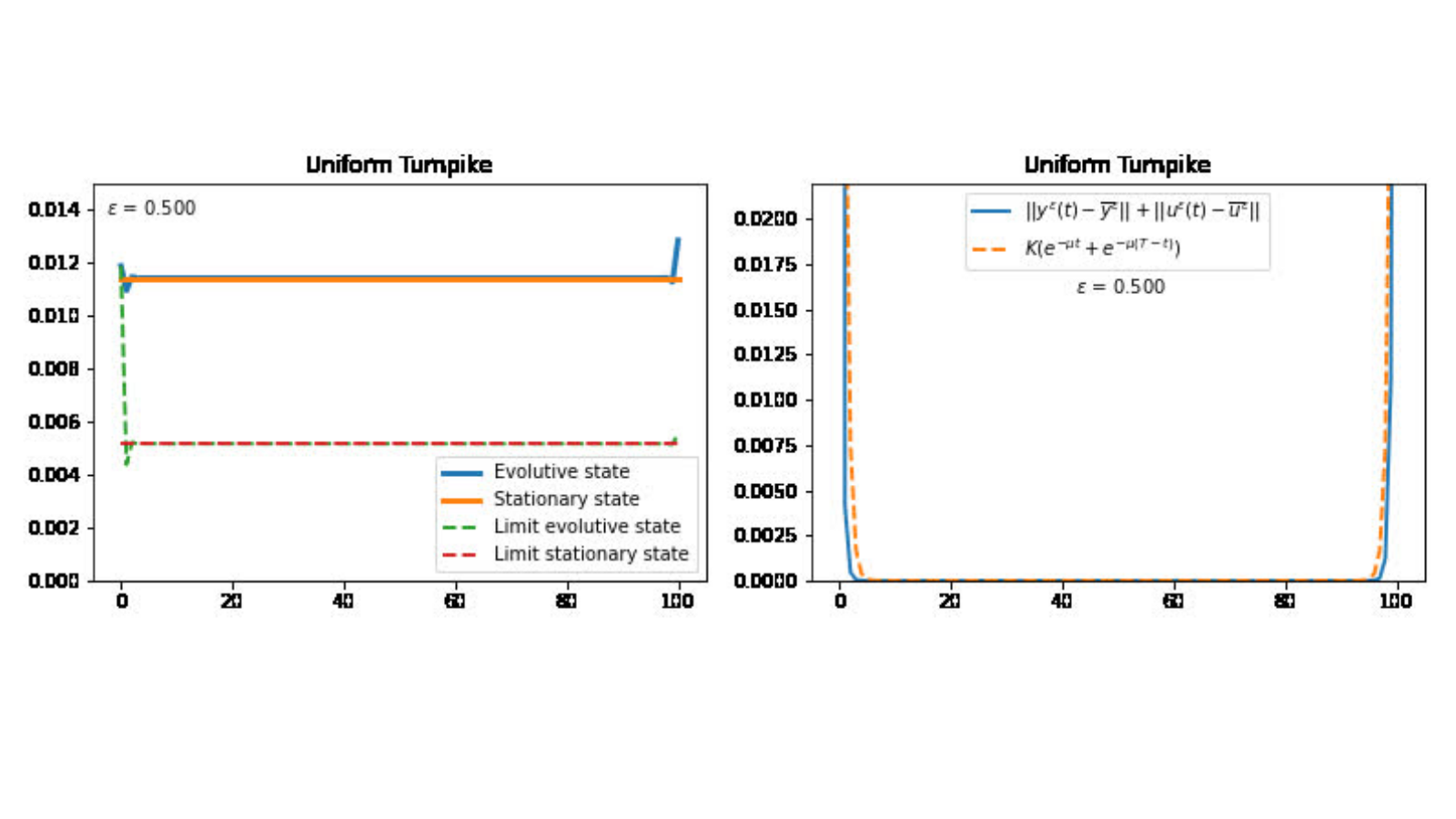
Uniform Turnpike Property 1 Introduction In this post, we analyze a heat equation with rapidly oscillating coefficients dependent on a parameter , with a distributed control. We show that the uniform null controllability implies the uniform turnpike property, i.e., the turnpike property with constants independent of the -parameter. The main […]
Author: Borjan Geshkovski, MIT The interplay of control and Deep Learning By Borjan Geshkovski It is superfluous to state the impact deep (machine) learning has had on modern technology, as it powers many tools of modern society, ranging from web searches to content filtering on social networks. It is […]
Nonlinear hyperbolic systems: Modeling, controllabiliy and applications The control theory of hyperbolic systems is an important topic in continuum and fluid mechanics. Networks of nonlinear hyperbolic systems arise in real world applications, e.g. planar or out-of-plane networks of vibrating strings, shearable beams, gas networks and shallow water systems. On these […]
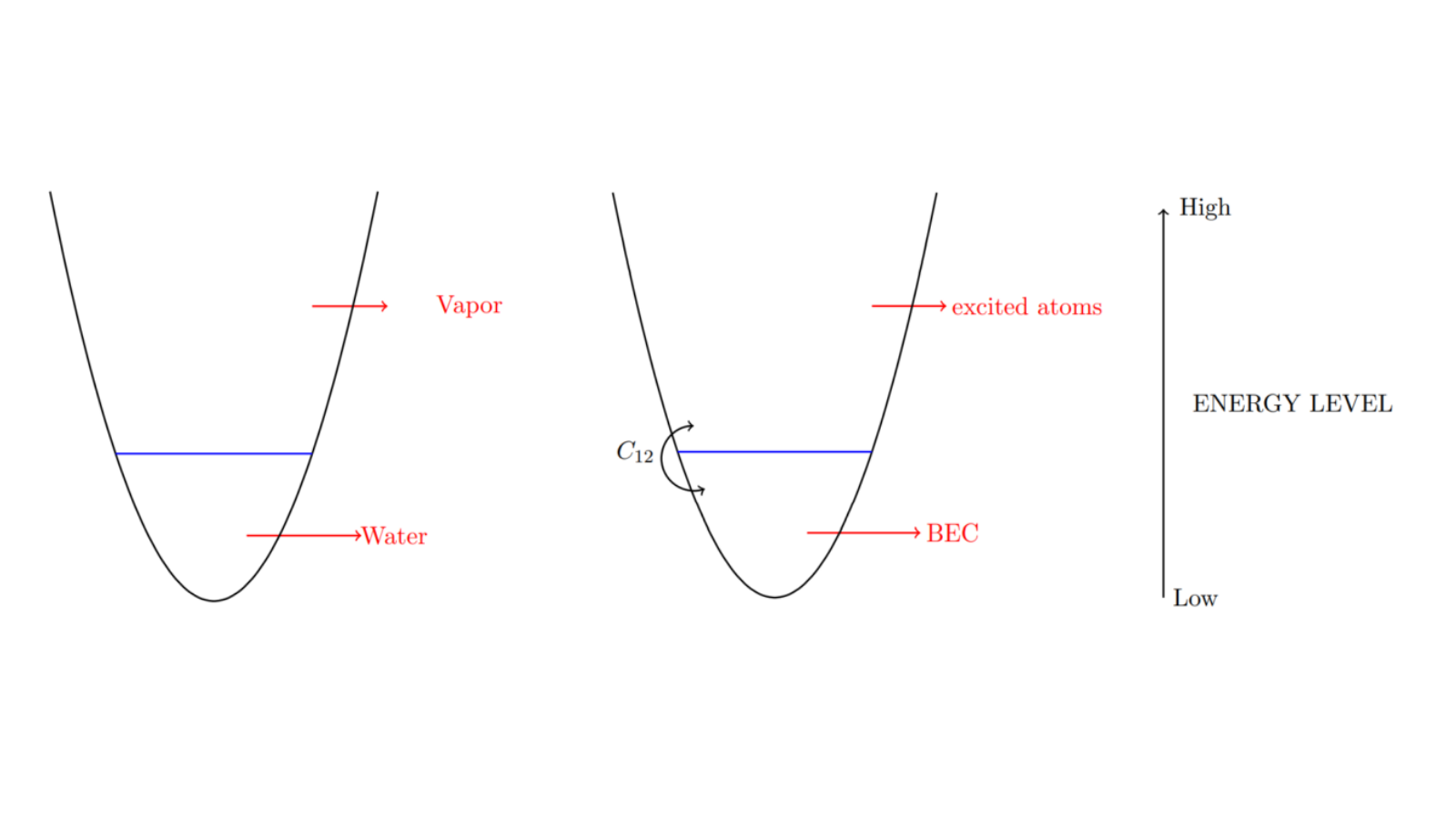
Kinetic theory of Bose Einstein Condensates If a dilute gas of bosons, about one-hundred-thousandth the density of normal air, is cooled to a temperature very close to absolute zero (0 K or -273.15C), the gas will be changed into a new state of matter, called Bose-Einstein condensate (BEC). This state […]
Author: Martin Gugat, Enrique Zuazua, Aleksey Sikstel, FAU DCN-AvH Code: [HINT] To run the software on your computer, you may have to install additional standard software packages (like cmake and a c++ compiler) and additional libraries (lapack, PETSc). In order to optimize the operation of gas transportation networks, […]
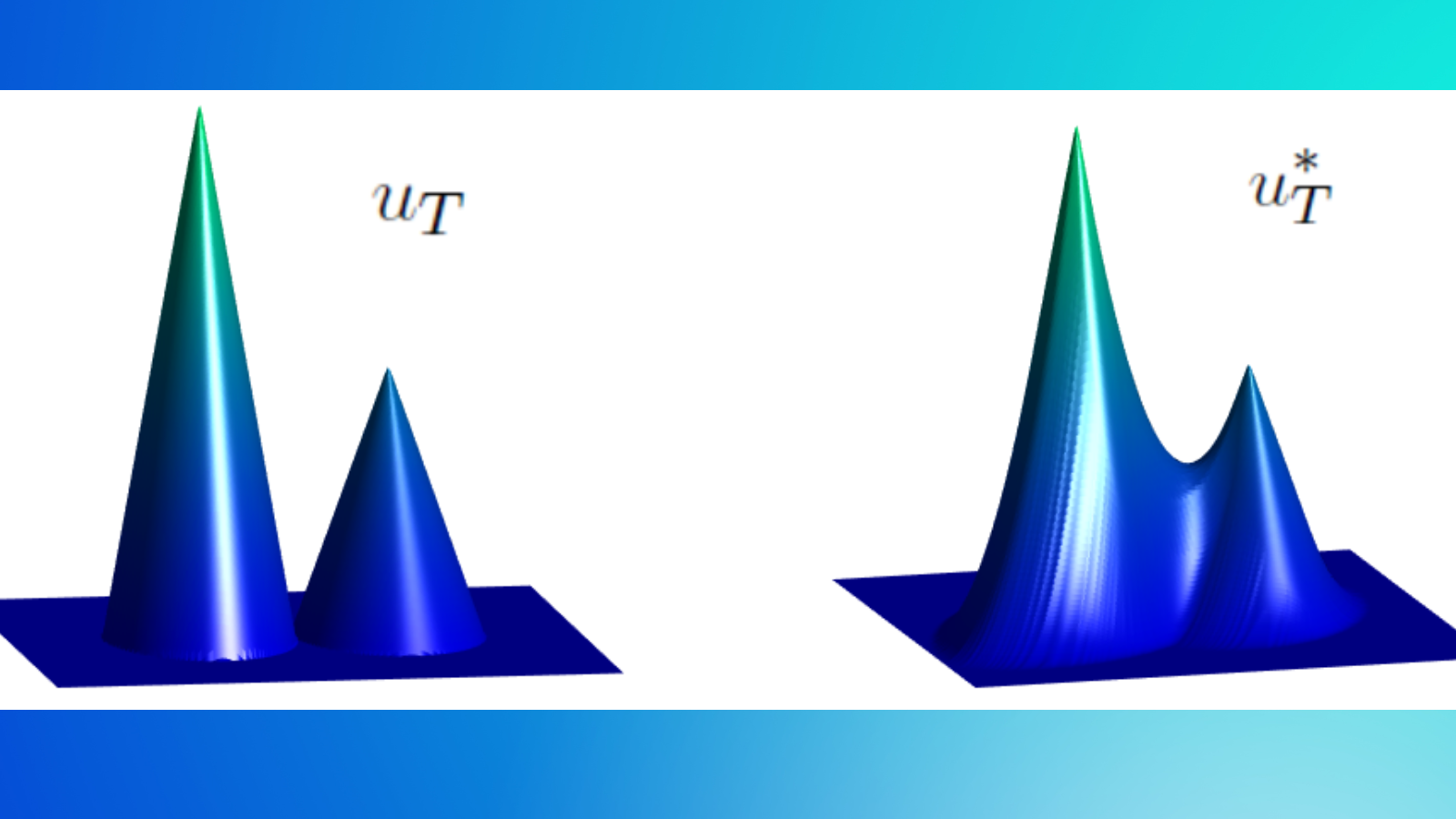
Author: Carlos Esteve, Deusto CCM Code: In a previous post “Inverse Design For Hamilton-Jacobi Equations“, described all the possible initial states that agree with the given observation of the system at time on the reconstruction of the initial state in many evolution models. Our goal here is to study the […]
Author: Daniel Veldman, FAU DCN-AvH Code: || Also available @Daniël’s GitHub In a previous post “Randomized time-splitting in linear-quadratic optimal control“, it was proposed to use the Random Batch Method (RBM) to solve classical Linear-Quadratic (LQ) optimal control problems. This contribution is concerned with the corresponding numerical implementation. We thus […]
Author: Alexei Gazca, FAU DCN-AvH Code: Below is a description of the types of problems that can be tackled using the code contained in this repository. Solving linear systems arising from the discretisation of partial differential equations can be an extremely challenging and computationally intensive task, especially for problems […]
Transition Layers in Elliptic Equations Stable transition layers in an unbalanced bistable equation Consider the following semi-linear problem where are positive functions in ; is a positive parameter and We assume that the functions satisfy ; for all ; there is a sub-interval such that for and for all […]
Randomized time-splitting in linear-quadratic optimal control By Daniël Veldman Introduction Solving an optimal control problem for a large-scale dynamical system can be computationally demanding. This problem appears in numerous applications. One example is Model Predictive Control (MPC), which requires the solution of several optimal control problems on a receding […]
Felix Klein: A Legacy of Innovation in Mathematics and Education By Roberto Rodríguez del Río, Complutense University of Madrid | IES San Mateo, Madrid Felix Christian Klein lived in a period of history of science in which Mathematics were involved in a process of transformation, leaving behind the classical […]
Control of Advection-Diffusion Equations on Networks and Singular Limits By Jon Asier Bárcena-Petisco, Márcio Cavalcante, Giuseppe Maria Coclite, Nicola de Nitti and Enrique Zuazua Introduction In the past few decades, models based on partial differential equations have been very effective in tackling many problems dealing with flows on networks (e.g. […]
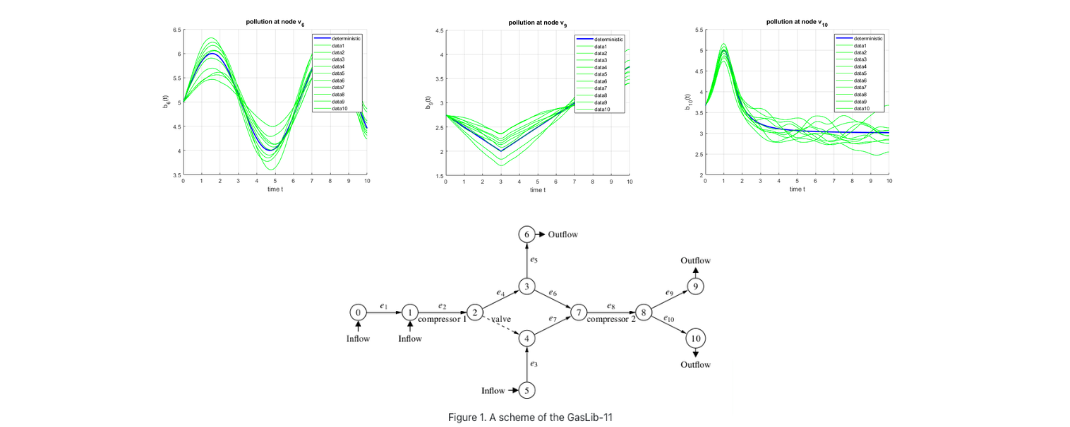
Probabilistic Constrained Optimization on Flow Networks This research was funded by DFG in the SFB Transregio 154: Mathematical modelling, simulation and optimization using the example of gas networks. Uncertainty often plays an important role in the context of flow problems. We analyze a stationary and a dynamic flow model […]
Perceptrons, Neural Networks and Dynamical Systems By Sergi Andreu // This post is last part of the “Deep Learning and Paradigms” post Binary classification with Neural Networks When dealing with data classification, it is very useful to just assign a color/shape to every label, and so be able to visualize data in a lower-dimensional […]
Deep Learning and Paradigms By Sergi Andreu // This post is the 2nd. part of the “Opening the black box of Deep Learning” post Deep Learning Now that we have some intuition about the data, it’s time to focus on how to approximate the functions that would fit that data. […]